Combining photons at a beam splitter and states tensorization

Question

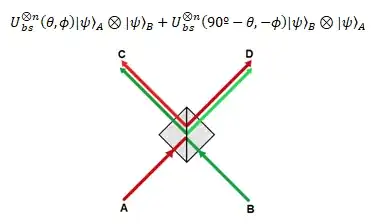
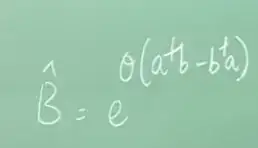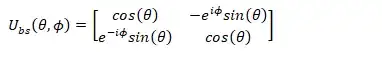I wonder what is the operation for 'combining' two polarized photons (one into each input arm, with perfect timing). I would consider three steps:

• 1.The two modes (polarization, arm) should be combined by tensor product (Left x Right states)

• 2.The BS matrix (Theta (R,T), Phi (phase)) should be applied to the previous tensor product

• 3.Symmetry arguments lead me to think that steps (1,2) should also be applied considering left/right inversion of the BS:

  3.1 Apply step 1 with operators in reverse order: Right x Left

  3.2 Apply step 2 with new_Theta = (90º - Theta), R and T are reversed , and new_Phi = - Phi, phase change is opposed.

If this is correct (which I'm pretty unsure) there would be two resulting states, which I would guess are added, in order to represent that the result at each output arm of the BS has a contribution from the two states previously calculated.

Any thoughts about these steps or this operation?

Answer 1

Finally, I am able to answer my own question. From the (fantastic) video-lecture by Lakshmi Bala, the beam-splitter operator is like this

Also, I have come to adapt the result to my own calculations like this:

1- A BS depends on two parameters: Theta, controlling the reflection and trasmission, and Phi, which introduces a phase shift between the reflected and transmited coefficients:

2 - For two states into the input ports of the BS, the resulting state is the superposition of applying the BS operator (U_bs) to every input state, noticing the complementary relations of Theta and the sign inversion of Phi between the two input ports, due to the change of components that are reflected and transmited by the BS. Also, every input must be combined with the other by tensor product, and the U operator must also be tensor-multiplied by itself in order for the states and the operator to have the same dimensions.