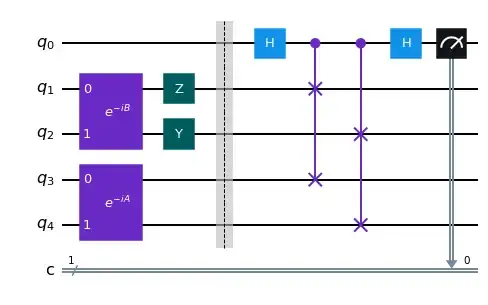
From this SE question and this Qiskit tutorial, I understand how to compute the expectation such in the form of $\langle \psi|H|\psi\rangle$ or $\langle 0^{\otimes n} |e^{iA} H e^{-iA}|0^{\otimes n} \rangle$ . But what about efficiently computing $\langle 0^{\otimes n} | e^{iA} H e^{-iB} |0^{\otimes n} \rangle$ when $A$ and $B$ are different and have more than single Pauli term in a quantum computer? $A$, $B$, and $H$ can be assumed to be Hermitian since that is the usual condition in such problem. Also, let us say we know $H$ as the linear combination of Pauli basis (i.e., Pauli decomposition of $H$).
I can certainly use Hadamard test to achieve my goal, but the circuit depth will be very large when $A$ and $B$ are composite of multiple Pauli terms, even use order-1 Suzuki trotterization to trotter $e^{iA}$ and $e^{-iB} $.
Also, if I want to use Qiskit functions like PauliExpectation() and CircuitSampler to do the computation, it seems like $e^{iA} H e^{-iB}$ is never involved with any quantum techniques but computed classically. Here is why I am saying this:
from qiskit.opflow import X, Y, Z, I
from qiskit import QuantumCircuit
from qiskit.opflow import CircuitStateFn,PauliExpectation,CircuitSampler
from qiskit.opflow import StateFn,PauliTrotterEvolution,Suzuki
from qiskit.providers.aer import AerSimulator
from qiskit.utils import QuantumInstance
Backend
backend = AerSimulator(method='statevector')
q_instance = QuantumInstance(backend, shots=1024)
sampler = CircuitSampler(q_instance)
Operators
A = (0.6Z^X) + (0.1Z^Y)
H = (0.3I^Z) + (0.6Y^Z)
B = (0.1I^Y) + (0.6Y^X)
op = A.exp_i().adjoint() @ H @ B.exp_i() # e^{iA} H e^{-iB}
obs = StateFn(op).adjoint() # let Qiskit consider this as the observable
Initial State |00>
init_state = QuantumCircuit(2)
init_state = CircuitStateFn(init_state)
Compute expectation
measurable_expression = obs @ init_state
trotterized_op = PauliTrotterEvolution(trotter_mode=Suzuki(order=1, reps=1)).convert(measurable_expression)
expectation = PauliExpectation().convert(trotterized_op)
sampled_exp_op = sampler.convert(expectation)
print("Expectation:", sampled_exp_op.eval())
The printout will be
Expectation: (0.008744335460630945-0.015886672611238318j)
It looks good so far, but if I check how many and what circuits executed in the simulator
print(len(list(sampler._circuit_ops_cache.values())))
It will give
1
which is just the circuit for state $|00\rangle$
So in this case, I suppose Qiskit only use the quantum circuit to obtain init_state, and no quantum techniques, like qubit-wise commutativity, is applied. Of course, if one changes A and B to a single Pauli term, then sampler._circuit_ops_cache.values() will store multiple circuits and qubit-wise commutativity is indeed applied.