How to train a custom parameterized circuit with multiple parameters and intermediate measurements?

Question

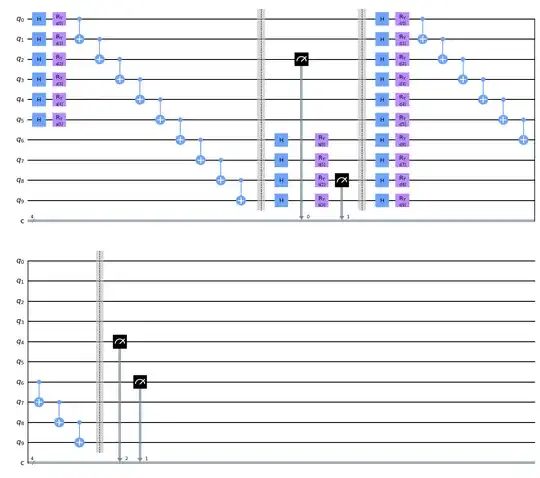
from qiskit import *
from qiskit.circuit import *
from qiskit.visualization import *
from qiskit.circuit.library import *
from qiskit.quantum_info import *
from qiskit.circuit.library import *
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
QC = QuantumCircuit(10,4)
Qs = ParameterVector('a', 6)
for i in range(6):
    QC.h(i)
    QC.ry(Qs[i], i)
for i in range(9):
    QC.cx(i, i+1)
QC.barrier()
Ps = ParameterVector('b', 4)
for i in range(4):
    QC.h(i + 6)
    QC.ry(Ps[i], i + 6)
QC.measure(2,0)
QC.measure(8,1)
QC.barrier()
Qs = ParameterVector('c', 10)
for i in range(10):
    QC.h(i)
    QC.ry(Qs[i], i)
for i in range(9):
    QC.cx(i, i+1)
QC.barrier()
QC.measure(4,2)
QC.measure(6,1)
QC.draw('mpl')

Answer 1

You can train it using a classical optimizer just as in quantum circuits without measurement. As long as you have an objective function, you can try using scipy.optimize or other classical optimizers.

Check out this post for a good example. The example doesn't include measurement, but as long as you can feed a single number into the optimizer you're ready to start optimizing.