Is there a gate sending $|0\rangle^{\otimes n}$ to a state where some amplitudes are zero?

Question

By preparing $n$ qubits in $|0 \rangle ^{\otimes n}$ and then passing through the Hadamard gate, one can obtain a system superposition in $\{0,1 \}^n$, each state with equal probability.

I’m wondering if it’s possible to prepare the system in a state where some of the states $|i\rangle$ have a probability of zero.

And $i$ need not be constant in some digit.

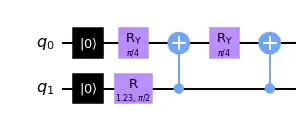
Using two qubits as an example: input $|00 \rangle$, expecting $|\psi \rangle = \frac{1}{\sqrt{3}}(|10\rangle +|01\rangle+|00\rangle)$. Do there exists some gate doing this?

poig · Answer 1 · 2022-06-06T13:07:35.877

you can check out qiskit textbook,

This is how you do it:

import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, assemble, Aer
q = QuantumRegister(2, name = 'q')
circuit = QuantumCircuit(q)
#Define initial state

initial_state = [1/np.sqrt(3), 1/np.sqrt(3),1/np.sqrt(3),0]

circuit.initialize(initial_state, [0,1])
circuit.decompose().decompose().decompose().decompose().decompose().draw("mpl")

Is there a gate sending $|0\rangle^{\otimes n}$ to a state where some amplitudes are zero?

1 Answers1