A financial firm has criticized the quantum computer of a company called IonQ.
Part of the content is that IonQ's quantum computer is only 60% accurate for 1+1 calculations, and only 50% for 2+3 calculations.
And they said it was garbage.
Is this low accuracy compared to other quantum computers?
What about ibm or honeywell?
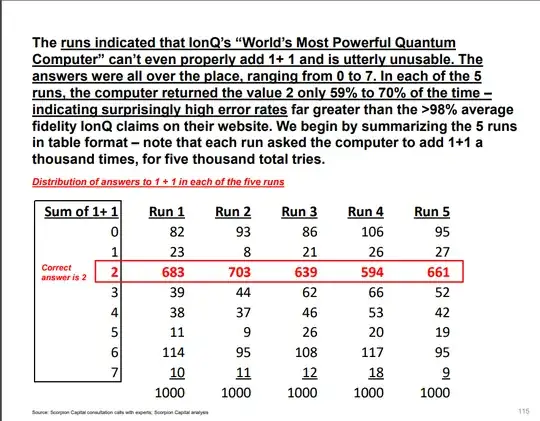
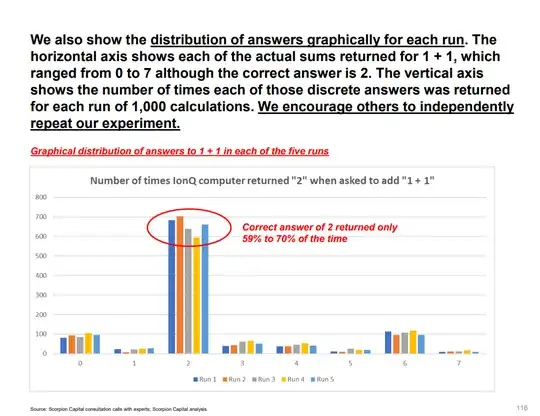
60% accuracy on a 3 bit adder is about the right ball park for modern quantum computers.
I don't know how they decomposed their 3-bit adder, but they probably used 50 to 100 gates. For scale, n-bit addition is slightly harder than (n+1)-bit incrementing and the best 4 bit incrementer I know needs 30 gates. Current error rates are between 0.1% and 1% per gate, and if you incur that error 50 to 100 times it's easy to be wrong 40% overall.
And yes it's consistent with what you see on other computers. For example, here's what I got from trying to count by repeatedly applying an incrementer:
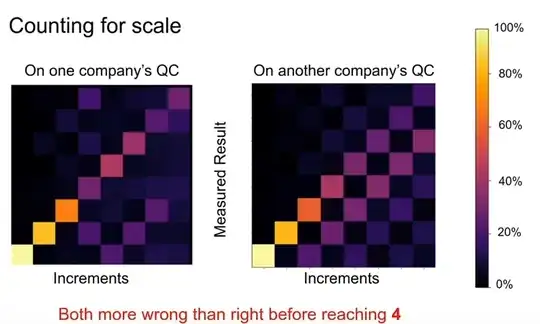
This is not surprising new information to anyone in the field, by the way. Go ask any researcher how high they think a quantum computer can count today, and they'll give an answer less than 10. Go look at any public company road map and it will have quantum error correction on it, to deal with this problem.
