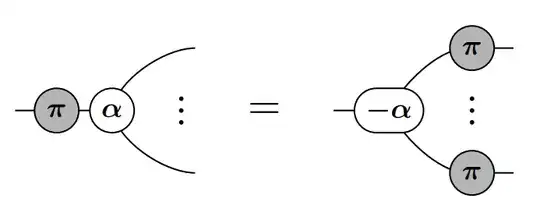
In the ZX-calculus we have the following rule, which I think it is known as the copy-rule (grey/white colours may be interchanged; with respect to the usual red/green notation the translation is white equivalent to green and grey equivalent to red):
Now, my question is the following: Given that in the ZH-calculus (see same reference from above, or also this reference) we have H-boxes that are 'similar' to spiders in the ZX-calculus, can we have something like the rule from above?
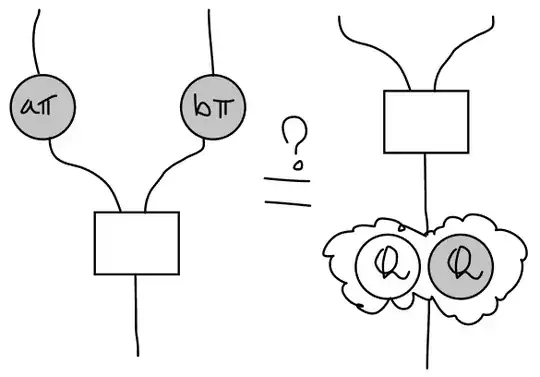
To be concrete, I have in mind exactly if the following is possible for some gate (or sequence of gates) $\mathcal{Q}$ (probably a function of $a\pi$ and $b\pi$, probably grey?)
In words, above is that I want a way to pass through the gates into the H-box.
My attempt: I don't think it is possible because if we consider for instance two grey $\pi$ gates, they correspond to $X\otimes X$ gates and hence we have that the equation would read as matrices something like,
$$ (\text{H-box})\circ \left(\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}\right)^{\otimes 2} = \left(\begin{matrix}1 & 1 & 1 & 1 \\1 & 1 & 1 & -1\end{matrix}\right)\left(\begin{matrix}0 & 0 & 0 & 1 \\0 & 0 & 1 & 0 \\0 & 1 & 0 & 0 \\1 & 0 & 0 & 0 \end{matrix}\right) = \left(\begin{matrix}1 & 1 & 1 & 1 \\-1 & 1 & 1 & 1\end{matrix}\right)$$
And I don't think there exists a sequence of matrices that can be applied to send the $-1$ factor back to where the H-box originally had. Certainly a single $2\times 2$ matrix cannot do this. But I wonder if other combinations would make it possible.