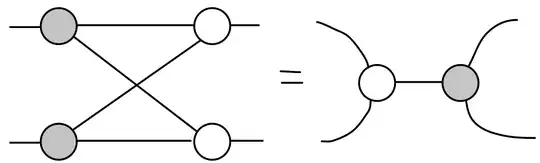
In the ZX-calculus, one of the fundamental rules of the diagrammatic reasoning is known as the bialgebra rule and it is described by the given diagrammatic equation:
Question: Can we implement this diagram without using post-selection or adaptivity?
I know that this rule preserves the gflow of a diagram, which implies that if a circuit is transformed to a ZX-calculus diagram and after simplification this rule is used then the resulting ZX-diagram can be transformed back into a quantum circuit. But from what I could understand, the bialgebra seems to preserve the gflow but it is not directly circuit implementable (i.e. with unitaries) because there is a $2 \to 1 \to 2$ qubit flow that must result in measurement. Hence, any non-adaptive and non-postselected implementation likely must come from not using single two systems but a possibly more complex system.
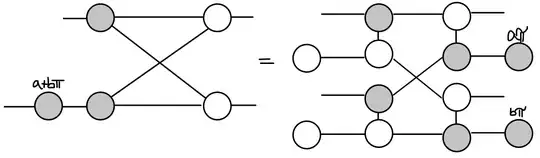
The adaptive implementation of the bialgebra (left side of the diagram) is very interesting but I think that it would be more interesting to have a circuit implementing. Moreover there is the $a\oplus_2b\pi $ term in the beggining that is very complicated to get rid of.
In this question, notation and reference to known results were taken from Ref. ZX-calculus for the working quantum computer scientist. The last diagram is mine so it might have mistakes.