I'm studying Shor's algorithm and I'm wondering how to build the quantum circuit for the modular exponentiation calculation in the Shor's algorithm.
Is the circuit found classically (using conventional computers) by checking the truth table of the modular exponentiation calculation result?
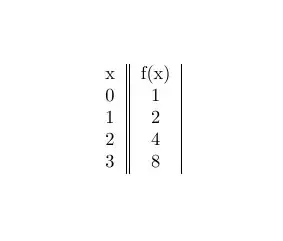
For example, when I try to run the Shor's algorithm for factoring N=15 with a randon number a=2, the truth table of the modular exponentiation function $(f(x)=2^xmod15)$ looks like below:
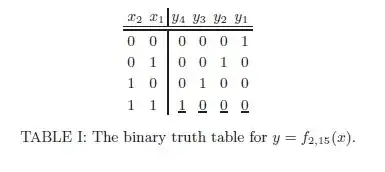
In binary representation, the truth table looks like below:
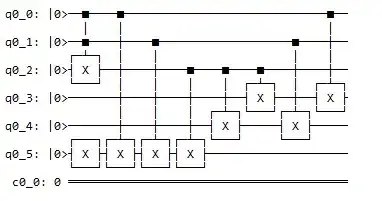
The quantum circuit for this truth table looks like below:
Is the quantum circuit for this calculation found by conventaionl classical computers?