For transmon qubits, there is an always-on zz interaction between coupled qubits, thus introducing static zz crosstalk. The figures are from this paper. I know zz crosstalk can change the frequency of the spectator qubit (Q2 in the figure).
My question is: since zz crosstalk is always on, why is there a difference of frequency for Q2 when Q1/Q3 is set to 0 or 1 state? (second figure)
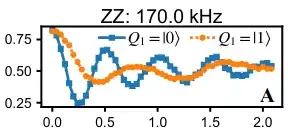
the difference in frequency is precisely because the interaction is always on.
Let's start with a scenario where there is no ZZ interaction. In this case, the Hamiltonian during the free evolution time is simply
$$ H=\sum_{i=1,2,3}\frac{1}{2}\hbar\omega_{i}\sigma_{zi}. $$ Then the phase accumulated during the free evolution time for qubit 2 is $\omega_2 \Delta t$, where $\Delta t$ is the free evolution time, regadless of the state of qubits 1 and 3.
If, however, we include ZZ interaction (and assuming for simplicity we only have qubits 1 and 2), the Hamiltonian becomes: $$ H=\sum_{i=1,2}\frac{1}{2}\hbar\omega_{i}\sigma_{zi} + \frac{1}{2}J\sigma_{z1}\sigma_{z2}. $$ Now, if we set qubit 1 to the $|0\rangle$ state, the evolution seen by qubit 2 is effectively $$ \langle0|H|0\rangle=\frac{1}{2}(\hbar\omega_{2}+J)\sigma_{z2} $$ and so the phase accumulated during free evolution will be $(\omega_2 +J )\Delta t$. If, on the other hand, the state is $|1\rangle$, the accumulated phase will be $(\omega_2 -J )\Delta t$. This is the origin of the change in oscillation frequency in the figure above.
