7

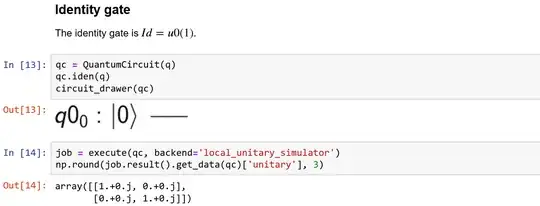
I found it odd that the result of the action of identity gate (namely a $2\times2$ identity matrix) on a pure state $|0\rangle$ (namely the vector corresponding to the $2\times1$ matrix $\begin{bmatrix} 1\\0 \end{bmatrix}$) becomes a $2\times2$ matrix $\begin{bmatrix} 1+0\cdot i&0+0\cdot i\\0+0\cdot i&1+0\cdot i \end{bmatrix}=\begin{bmatrix} 1&0\\0&1 \end{bmatrix}$ as I found it HERE (QISKit tutorial page): 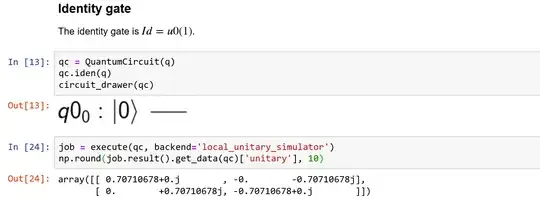enter image description here

Also, when one lets for more precision, the result gets odd:

enter image description here

Why is this? The same thing happens for other gates listed on the page referenced above.

user1271772 No more free time
  • 14,286
  • 2
  • 26
  • 76
Mathist
  • 495
  • 3
  • 11

1 Answers1

3

In the first case you are not asking for the state but the unitary matrix representing the circuit. This is correct and just rounding error. It looks like you are not using the latest version so I would update.

In the second case are you sure that you don’t have a previous circuit loaded in memory. In that notebook all examples have the same circuit name and it looks like this is a different gate. If i had to guess it is the u2 example. If this is not the case you have found a bug and please submit an issue and we try to debug it.

I would also change the title as this is not a general quantum computing question to one qubit gates errors in qiskit or something like that.

Jay Gambetta
  • 571
  • 2
  • 6