Grover's algorithm for 3SAT problem gives unexpected results

Question

Based on SAT problem and Grover's algorithm, I've done some experiments. For the below example, I've received unexpected results:

1. Input: boolean function:

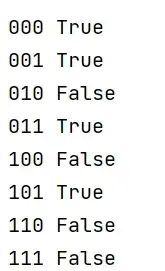
   c example 4
   p cnf 3 4
   1 -2 -3 0
   1 -2 3 0
   1 2 -3 0
   -1 -2 -3 0
   

2. Truth table of boolean function:

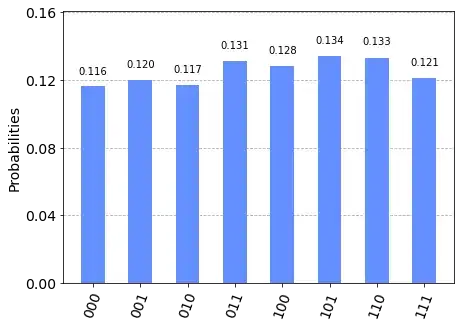
3. Histogram of results

According to the truth table, the results should be ['000', '001', '011', '101']. Why does the algorithm not return the expected solutions?

EDIT: Regarding the first comment. I've noticed that for boolean function:

c example 3
p cnf 3 3
1 -2 -3 0
1 -2 3 0
1 2 -3 0

We get the correct results. In this example $M>N/2$.Additionally, I've noticed that the first example is a balanced function and the second one is not. Is it relevant?

Answer 1

This issue happens because $M \geq \frac{N}{2}$, where $M$ is the number of solutions and $N$ is the search domain size. For more details see this answer.

A workaround is to double the search domain by adding a dummy variable:

c example 4
c Add one to <#vars> and <#clauses>
p cnf 4 5
1 -2 -3 0
1 -2 3 0
1 2 -3 0
-1 -2 -3 0
c Add a clause for the dummy variable
-4 0

For you second example, 3 out of 5 solutions will be returned if the optimal number of iterations is used ($\Big\lfloor \frac{\pi}{4} \sqrt{N/M}\Big\rfloor$). You can get all the solutions by changing the number of iterations:

grover = Grover(iterations = 2, quantum_instance=quantum_instance)

Doing the same for the first example will not work (see the figure in this answer). However, doubling search domain should always work.