when calculating code thresholds, why do we need to take a number of rounds that scales with the code distance?

Question

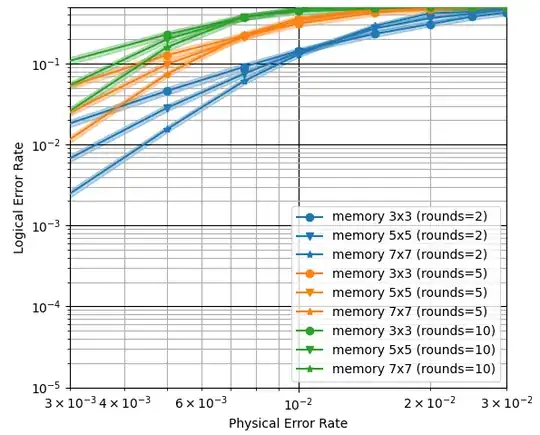
In stim's error corretion example here, and in pymatching's toric code example here, the threshold calculation involves taking a number of rounds that scales as the code distance. Why is that the right way to do it?

To test what's going on if I try to do it some other way, calculated the threshold with a fixed number of rounds, yet much larger than the distance, and I get something that behaves reasonably until some "pseudo threshold" value, and then the errors seem to more or less track each other. How can we explain this behavior?

Here's an example of a surface code with rounds = 3 * distance as in the stim example:

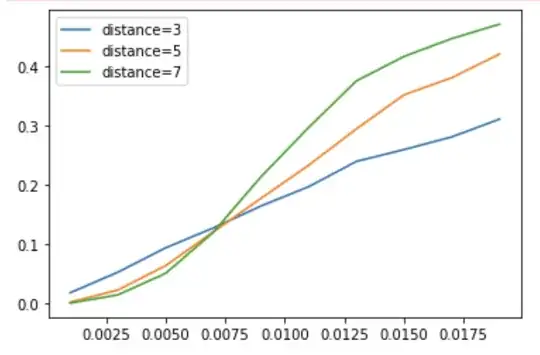
and here's one with rounds=20:

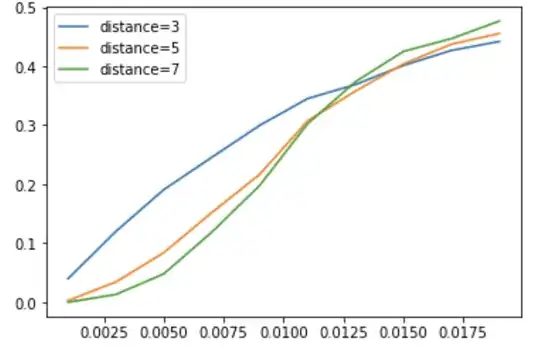
The x axis are physical (2 qubit gate) error rates, and the y axis is logical error rate

BTW, I have a vague feeling that this is somehow related to this question.

Answer 1

(Note: you should take more data so those curves have less noise. You might also want to plot standard deviations of some sort so you can see the noise. The Stim example keeps to really low rep rates so it finishes in under a minute, not because that's recommended.)

The reason you want more and more rounds is because of boundary effects. Near boundaries, whether they be spatial boundaries or temporal boundaries (data initialization and measurement), the number of possible error chains is lower than in the bulk. Because errors that would have careened around without a care in the world instead slam into a wall. As the code distance gets bigger, the relevant error chains get longer, so the boundaries need to be further and further away. The threshold people are usually interested in is the threshold of the bulk, with boundaries nowhere nearby, and these can be different values.

You can very clearly see the problem at low round numbers. The threshold for 2-round memory experiments is higher than for 5-round memory experiments which is higher than for 10-round memory experiments. Here's data I took which agrees with your data. Note how the three curve groups have their respective crossings at different horizontal locations:

Incidentally, this is one of the reasons error correction experiments that do repetitive measurement instead of a single-shot thing are much more impressive. Single-shot experiments are like setting the number of rounds to 1, and have a much easier threshold.