Universal quantum computation by Clifford gates plus magic state

Question

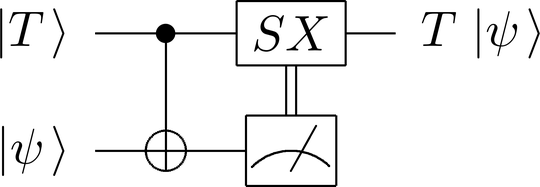
In the paper Universal quantum computation with ideal Clifford gates and noisy ancillas, it is claimed that a circuit composed by Clifford gates, plus a so-called "magic state", can perform any quantum computation.

This paper is based on the formalism developed for fault tolerance. However, the claim above does not have to do with fault tolerance, nor with "noise". Indeed, the section III, which discusses the universal quantum computation, does not even mention the "noise" and the magic state is simply a well-defined pure state. It looks like it is possible to build any circuit using Clifford gates and simulating the T gate by using the so-called magic state, which is simply $\alpha\left|0\right>+\beta\left|1\right>$ with well defined $\alpha$ and $\beta$ (together with a particular procedure and additional Clifford gates).

So I would like to understand what I miss, if I do not understand the discussion about the fault tolerance and noisy qubits. Looking in literature, I feel that I actually miss something. For example, here I read this sentence:

quantum computers with magic states will most likely have the vast majority of its usable qubits be used for the distillation of magic states

Thus it seems that this "distillation" is needed: is it simply the preparation of $\alpha\left|0\right>+\beta\left|1\right>$ with known $\alpha$ and $\beta$?

So I would like to have a sketch of the idea of the relation between the discussion on universal computation and fault tolerance, or a reference discussing this idea more in depth but without relying too much on the language of fault tolerance.

Answer 1

From Sec. V on in the Bravyi-Kitaev paper, it is all about noise - in particular magic state distillation, which is the process of distilling the magic state from many copies of some noisy state $\rho$.

Let us zoom out a bit. The magic state gadget replacing the $T$ gate looks like the following:

If we can do the Clifford gates and the measurement fault-tolerantly, which we can for a suitable stabilizer code, this circuit is fault-tolerant. However, the problem is that the preparation of the magic state $|T\rangle = \frac{1}{\sqrt{2}}(|0\rangle + e^{i\pi/4}|1\rangle)$ might not be.

So how would you prepare such a state?

1. First, one can observe that $|T\rangle$ is the +1 eigenstate of a suitable Clifford unitary $U$. Hence, by preparing e.g. a logical $|0\rangle$ state and then measuring in its eigenbasis (applying $U^\dagger$ to $|0\rangle$, then measuring in the computational basis), we get either the +1 or -1 eigenstate as post-measurement state. Post-selecting on the +1 outcome results in $|T\rangle$. This is actually fault-tolerant, but the physical error rate can be quite high, so you would have to repeat very often (see e.g. the discussion on p. 3 in "Roads towards fault-tolerant universal quantum computation" by Campbell, Terhal, and Vuillot).

2. You prepare a noisy approximation $\rho$ to $|T\rangle$, somehow. Then you use a magic state distillation protocol to distill a better approximation to $|T\rangle$ from $\rho^{\otimes n}$. In fact, it is enough to use stabilizer protocols only, i.e. protocols which only use stabilizer circuits. This is also interesting from a foundational perspective: Which states can you actually distill and which not? This is discussed in the Bravyi-Kitaev paper. Unfortunately, magic state distillation is also very costly.

I think the discussion of fault-tolerance in Nielsen & Chuang is not such a bad reference to begin with. In particular, Chapter 10.6 and the section "Fault-tolerant $\pi/8$ gate" on page 485. Unfortunately, magic state distillation is not discussed there.