Kernel ridge regression with qiskit's FeatureMap shows nonlinear patterns outside [0,1] range

Question

I'm implementing a kernel ridge regressor using qiskit's FeatureMap and QuantumKernel to compute the alpha parameters of the solution. If I try to fit my model with non-normalized features I obtain strange, nonlinear patterns in my predictions. To compute my solutions I'm using the default formulation I found here

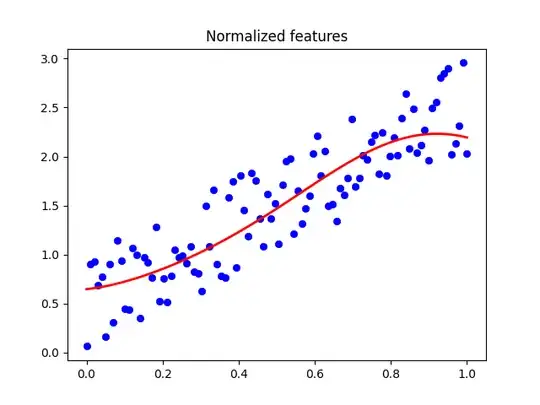
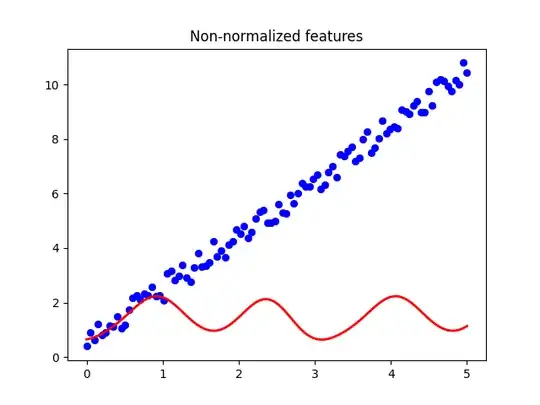
This is the code I used to produce these results:

from qiskit import BasicAer
from qiskit.circuit.library import ZFeatureMap
from qiskit.utils import QuantumInstance
from qiskit_machine_learning.kernels import QuantumKernel
import numpy as np
import matplotlib.pyplot as plt
class QuantumRidge:
    def init(self, gamma, quantum_instance, feature_map):
        self.q_kernel = QuantumKernel(feature_map=feature_map,
                                 quantum_instance=quantum_instance)
        self.gamma = gamma
def fit(self, X_train, y_train):
    self.X_train = X_train
    n_train = y_train.size
    I = np.eye(n_train)
    K_train = self.q_kernel.evaluate(x_vec=X_train)
    K_train = K_train + self.gamma * I
    self.alpha = np.linalg.solve(K_train, y_train)

def predict(self,X_test):
    K_test = self.q_kernel.evaluate(self.X_train, X_test).T
    prediction = K_test @ self.alpha
    return prediction


quantum_instance = QuantumInstance(BasicAer.get_backend('statevector_simulator'), shots=512)
feature_map = ZFeatureMap(2)
x_lin = np.linspace(0, 1,100).reshape(-1,1)
Normalized
qr_norm = QuantumRidge(1,quantum_instance,feature_map)
X_norm = np.hstack([x_lin,x_lin])
y_norm = np.sum(X_norm,axis=1) + np.random.random(X_norm.shape[0])
qr_norm.fit(X_norm,y_norm)
y_pred = qr_norm.predict(X_norm)
plt.title("Normalized features")
plt.scatter(X_norm[:,0],y_norm,linewidth=0.5,c="b")
plt.plot(X_norm[:,0],y_pred,linewidth=2,c="r")
plt.show()
Scaled
scale = 5
qr_scaled = QuantumRidge(1,quantum_instance,feature_map)
X_scaled = np.hstack([x_lin,x_lin]) * scale
y_scaled = np.sum(X_scaled,axis=1) + np.random.random(X_scaled.shape[0])
qr_scaled.fit(X_scaled,y_scaled)
y_pred = qr_norm.predict(X_scaled)
plt.title("Non-normalized features")
plt.scatter(X_scaled[:,0],y_scaled,linewidth=0.5,c="b")
plt.plot(X_scaled[:,0],y_pred,linewidth=2,c="r")
plt.show()

Why does this happen? I suspect it's caused by the way QuantumKernel computes the matrix.

Answer 1

This is a result of the periodicity of the gates you use to encode your features. The circuit you have encodes a pattern $\mathbf{x} = (x_0, x_1) \in \mathbb{R}^2$ as \begin{equation} |\psi(\mathbf{x})\rangle = \left[(R_z(2 x_0) \otimes R_z (2 x_1) )(H \otimes H) \right]^2 |00\rangle \end{equation}

There's two issues here. First, since $R_z$ is $2\pi$-periodic in its arguments then this encoding only results in unique quantum states for, say, $\mathbf{x} \in \left[0, \pi\right] \times \left[0, \pi\right]$. While your second plot might look like it has a period around $\pi / 2$ it actually contains a lower frequency mode around $\pi$-periodicity as well; a larger support of the ridge regression function $\hat{f}$ on the higher frequency just happens to give slightly better MSE. You can verify this explictly reducing your feature map to reps=1 and seeing the $\pi$-periodic mode dominate after the $\pi / 2$ mode has disappeared with the second $R_z$ encoding layer - a consequence of the result$^1$ of (Schuld, 2020) where it was shown that circuits of this form$^2$ result in functions for which the size of the Fourier spectrum is linear in the number of encoding rotation gates.

On the other hand, no amount of additional layers will let you fit the the data beyond $x_0, x_1 = \pi$ as additional gates only adds higher frequencies. Consequently you need to rescale your data so that the lowest available mode of $f$ has a larger period.

---

$^1$ This idea was actually proposed earlier in (J Vidal, 2019) but their explanation is more obscure.

$^2$ The result actually applies to functions of the form $f(x) = \langle \psi(\mathbf{x}) | O | \psi(\mathbf{x}) \rangle$ for some Hermitian $O$ which isn't quite the same as $k(\mathbf{x}, \mathbf{x})$ and so the reasoning is less rigorous.