As stated in the question, I have found in several papers (e.g. 1, 2) that in order to perform a quantum walk on a given tree it is necessary to add some nodes to the root $r$, say $r^{'}$ and $r^{"}$. Why are they needed?
References:
Farhi E., "Quantum computation and decision trees". https://arxiv.org/abs/quant-ph/9706062
Ambainis A., "Any AND-OR formula of size N can be evaluated in time $N^{1/2+o(1)}$ on a quantum computer". http://www.ucw.cz/~robert/papers/andor-siamjc.pdf
Following up on and inspired by the comments from Rob, I sense that there's a bit of a similarity between, on the one hand, the boolean tree evaluation of Farhi and Gutmann (and of Ambainis et al.), and on the other hand, time-domain reflectometry (TDR) which is used to identify cracks/open circuits/short circuits/other faults on electrical cables.
For example, in TDR one may send a wave packet down a copper wire; if the wire is properly terminated, a fault along the wire will cause the wave packet to be reflected while a defect-free line may enable transmission. Similarly in the tree evaluation algorithms, one may partially flatten the tree.
In the tree evaluation algorithms, one may partially flatten the tree. One may also may add extra nodes to the root.
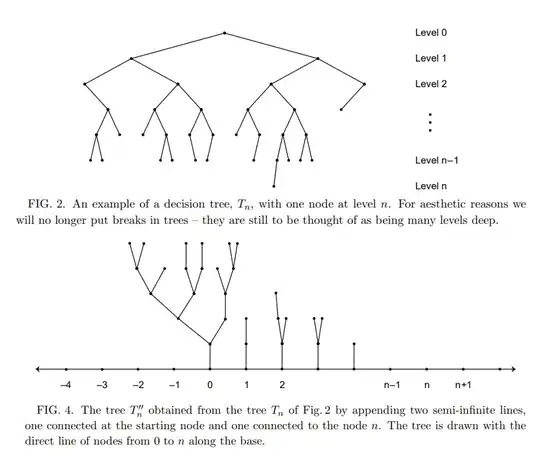
See, e.g., FIGS. 2 and 4 of Farhi and Gutmann, reproduced above.
Much as in TDR, if the tree evaluates to $0$ then a quantum wave packet will reflect back out from whence it came, whereas if the tree evaluates to $1$ then the wave packet will transit through the line.
If you didn't create your line by adding extra nodes to the root/flattening the tree, you would not have a way to send a wave-packet through the tree.
