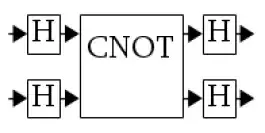
Step 1 (application of two hadamard gates):
$$|0\rangle_A \otimes |0\rangle_B \to \left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_A\otimes\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_B$$
This is equivalent to the state vector: $\begin{bmatrix}1/2\\1/2\\1/2\\1/2\end{bmatrix}$, which will act as the input for your CNOT gate.
Step 2: (application of CNOT)
Let's remind ourselves what the CNOT gate does:
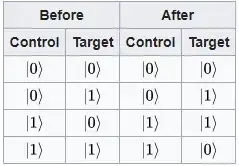
So clearly,
$$\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_A\otimes\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_B = \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle)$$ $$\to \frac{1}{2}(|00\rangle + |01\rangle + |11\rangle + |10\rangle) = \left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_A\otimes\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_B$$
Step 3: (re-application of two Hadamard gates)
$$\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_A\otimes\left(\frac{|0\rangle + |1\rangle}{\sqrt{2}}\right)_B \to |0\rangle_A \otimes |0\rangle_B$$
Here, we used that fact that the Hadamard gate maps the state $\dfrac{|0\rangle + |1\rangle}{\sqrt{2}}$ to the state $|0\rangle$, for each qubit. You basically need to input the vector $\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix}$ into the two Hadamard gates at the end. Find the state transformation on each qubit. From there you can construct the state vector for the final 2-qubit state. The final answer will be $\begin{bmatrix}1 \\ 0 \\ 0 \\ 0\end{bmatrix}$. Clearly, we end up with the same 2-qubit state which we started with.
Exercise: Carry out steps $2$ and $3$ using the matrix notation. Also, check this related answer.