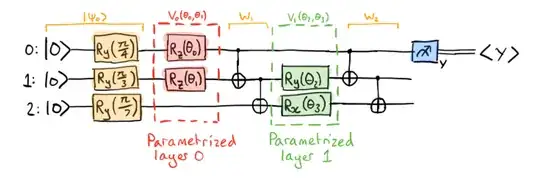
Following this paper and tutorial from Pennylane, I'm trying to re-calculate the Fubini-Study tensor:
$$ g_{i j}^{(\ell)}=\left\langle\psi_{\ell-1}\left|K_{i} K_{j}\right| \psi_{\ell-1}\right\rangle-\left\langle\psi_{\ell-1}\left|K_{i}\right| \psi_{\ell-1}\right\rangle\left\langle\psi_{\ell-1}\left|K_{j}\right| \psi_{\ell-1}\right\rangle $$ where $$ \left|\psi_{\ell-1}\right\rangle=V_{\ell-1}\left(\theta_{\ell-1}\right) W_{\ell-1} \cdots V_{0}\left(\theta_{0}\right) W_{0}\left|\psi_{0}\right\rangle $$
with:
$K_i$ is the generator of the parametrized operation. In this case, when calculating $g_{0,1}^{(0)}$, I understand that $K_0=K_1=-\frac{1}{2}Z$ with $Z$ is the 2x2 Pauli matrix. But $|\psi\rangle$ is the state of 3 qubits, so how to perform $g_{0,1}^{(0)}$? Or $K_0=-\frac{1}{2}Z\otimes I\otimes I$ and $K_1=-\frac{1}{2}I\otimes Z\otimes I$?
Thanks for reading!