Why isn't $Ry(\pi/2)$ gate equivalent to Hadamard gate?

Question

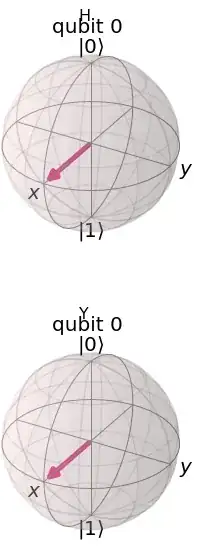
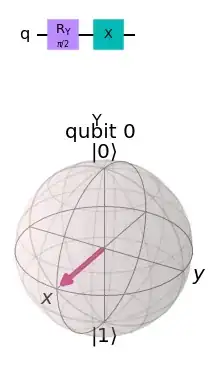
I've been experimenting with quantum circuits and can't quite fathom how the difference between states comes together.

Speaking in terms of simulations using qiskit, the following code yelds the same results:

circuit = QuantumCircuit(1)
circuit.h(0)
state = Statevector.from_instruction(circuit)
display(plot_bloch_multivector(state, title="H", reverse_bits=False))
circuit = QuantumCircuit(1)
circuit.ry(0.5*np.pi,0)
state = Statevector.from_instruction(circuit)
display(plot_bloch_multivector(state, title="Y", reverse_bits=False))

According to this page, the H-Gate is equivalent to the following circuit:

The state vector remains the same, which makes sense as it's only rotating around the x-axis.

Even negating the initial qubit state and make it a $|1\rangle$ does not bring any difference to the table.

So, I went deeper and looked at the maths behind it. Applying the H gate to $|0\rangle$ results in:

$$ H|0\rangle =\ \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} =\ \begin{pmatrix}\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}}\end{pmatrix} =\ \frac{|0\rangle + |1\rangle}{\sqrt{2}} =\ |+\rangle $$

Now, using the RY-Gate, we can construct a matrix using $\frac{\pi}{2}$. This is where my understanding of the mathematical application stops tho, and I can't quite figure out how to do the rest of the calculation. This is as far as I've come, but I can't quite "translate" the result into a comparable qubit state:

$$ \begin{pmatrix} \cos(\frac{\pi}{4}) & -\sin(\frac{\pi}{4})\\ \sin(\frac{\pi}{4}) & \cos(\frac{\pi}{4}) \end{pmatrix}|0\rangle =\ \begin{pmatrix} 0.707 & -0.707\\ 0.707 & 0.707\end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} =\ \begin{pmatrix} 0.707 \\ 0.707 \end{pmatrix} $$

Reason for this question is that I am trying different circuits to classify IRIS for comparison, and I am seeing much better accuracy when using my basic Y-Rotation based circuit in comparison to qiskits ZZFeature and RealAmplitudes circuit.

Answer 1

While Hadamard gate is defined as $$ H= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}, $$ $y$-rotation by $\pi/2$ leads to gate $$ Ry(\pi/2)= \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}. $$ So, there is a difference in position of -1 in the second column. Application of the $X$ gate returns the -1 in $Ry(\pi/2)$ to right place to obtain Hadamard gate.

You can easily see that $H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$ and $Ry(\pi/2)|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$. Application of $X$ after $Ry$ leads to the same quantum state.

However, while $H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$, $Ry(\pi/2)|1\rangle = \frac{1}{\sqrt{2}}(-|0\rangle + |1\rangle)$. Application of $X$ after $Ry$ switches states $|0\rangle$ and $|1\rangle$ and leads to $XRy(\pi/2)|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$.

This all means that $XRy(\pi/2)=H$.

Answer 2

The algebraic comparison of the operations is, of course, correct.

Additionaly, noting that $H$ is Hermitian, we see that $R_y\left(\frac{\pi}{2}\right)$ is not Hermitian, and must be transformed.

A more intuitive approach is to examine the effect of the rotations on the Bloch sphere. Note that the H gate is a rotation about an axis which is on the X-Z plane, in the middle between the X and Z axes, as shown:

When we perform a 90° rotation about the Y axis, $R_y\left(\frac{\pi}{2}\right)$:

We seem to have the correct result, namely $|0\rangle\rightarrow|+\rangle,|1\rangle\rightarrow|-\rangle$.

However, on closer inspection, we see that the original x axis is now pointing "down", whereas the H gate results in the x axis pointing up ($|+\rangle$ changing places with $|0\rangle$).

Moreover, if we apply $R_y\left(\frac{\pi}{2}\right)$ again, we get the wrong result: $|+\rangle \rightarrow |1\rangle$ instead of $|0\rangle$, and $|-\rangle \rightarrow |0\rangle$ instead of $|1\rangle$

Adding a $\pi$ rotation about the X axis, $R_x\left(\pi\right)=X$, "fixes" the resulting location of the X axis (pointing "up"), making the resulting operation correct (no effect on the $|+\rangle,|-\rangle$ states which are on the X axis, and flipping the $|0\rangle, |1\rangle$ states)

Answer 3

Just to emphasise the point on the accepted answer...

The two gates, when applied to a specific state, give the same output. That does not mean they are the same, because the action on another state may be different (and I don't just mean a global phase).

For example, if you take the state $|+\rangle=(|0\rangle+|1\rangle)/\sqrt{2}$ then $$ H|+\rangle=|0\rangle, $$ but $$ R_Y(\pi/2)|+\rangle=|1\rangle. $$ The two outcomes are orthogonal. So, in this case, you can definitely tell which of the two you have just by measuring the output.