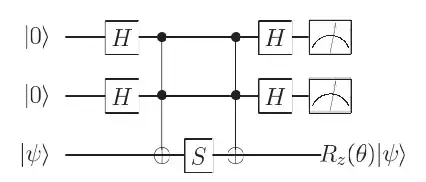
Part 1
The final output state is,
$|\psi_{out}\rangle=\frac{1}{4}[|00\rangle(3S+XSX)|\psi\rangle+|01\rangle(S-XSX)|\psi\rangle+|10\rangle(S-XSX)|\psi\rangle+|11\rangle(-S+XSX)|\psi\rangle]$
When the measurement outcomes are both 0 then the circuit applies $R_z(\theta)$ to the 3rd qubit where $\theta$ is such that $\cos\theta=3/5$, and otherwise applies $Z$ to the 3rd qubit, i.e., $$ (3S+XSX)|\psi\rangle=\sqrt{10}\begin{bmatrix}\frac{3+i}{\sqrt{10}}&0\\0&\frac{1+3i}{\sqrt{10}}\end{bmatrix}|\psi\rangle=\sqrt{10}e^{i\pi/4}R_z(\theta)|\psi\rangle $$
$$ (S-XSX)|\psi\rangle=(\begin{bmatrix}1&0\\0&i\end{bmatrix}-\begin{bmatrix}i&0\\0&1\end{bmatrix})|\psi\rangle=\begin{bmatrix}1-i&0\\0&-1+i\end{bmatrix}|\psi\rangle=e^{-i\pi/4}\begin{bmatrix}1&0\\0&-1\end{bmatrix}|\psi\rangle=e^{-i\pi/4}Z|\psi\rangle $$
The final output state can be rewritten as,
$|\psi_{out}\rangle=|00\rangle\frac{\sqrt{10}e^{i\pi/4}}{4}R_z(\theta)|\psi\rangle+(|01\rangle+|10\rangle-|11\rangle)\frac{e^{-i\pi/4}}{4}Z|\psi\rangle$
where $\theta$ is such that $\cos\theta=3/5$ and it is an irrational jultiple of $2\pi$
The probability that both measurement outcomes being 0 is $5/8$, i.e., $P(00)=\Big|\dfrac{\sqrt{10}e^{i\pi/4}}{4}\Big|^2=\dfrac{5}{8}$
Part 2
If you get any of the measurement results $01, 10$ or $11$, the output state is $Z|\psi\rangle$, then $Z$ is applied and the state is back to the initial state $|\psi\rangle$ and the circuit is repeated. If the measurement outcome is $00$ the output is $R_z(\theta)|\psi\rangle$ and the circuit is terminated.
After $k$ repetitions of the circuit the probability of success is, i.e., probability of obtaining $R_z(\theta)|\psi\rangle$, $$ \frac{5}{8}+\frac{5}{8}.\frac{3}{8}+\frac{5}{8}.(\frac{3}{8})^2+\frac{5}{8}.(\frac{3}{8})^3+\cdots=\frac{5/8(1-(3/8)^k)}{1-3/8}=1-(3/8)^k $$ which tends to $1$ as $k$ becomes large, i.e., we have a circuit which may be used to apply $R_z(\theta)$ gate with probability approaching $1$.
Using the above construction how do we show that the Hadamard, phase, controlled-NOT and Toffoli gates are universal for quantum computation ?
My thinking : Any single qubit unitary can be written as $R_z(\alpha)R_x(\beta)R_z(\gamma)$ upt an unimportant global phase factor, so if we can construct $R_x(\theta)$ from $R_z(\theta)$ then we can construct any unitary gate.
Refer to Exercise 4.43, Page 198, Quantum Computation and Quantum Information by Nielsen and Chuang