2

I was confused about something related to quantum $1$ designs.

Let us recap two facts we know about random circuit ensembles that form a $1$ design.

  1. $1$ design, for a quantum circuit over $n$ qubits, means that the density matrix of the ensemble is equal to the maximally mixed state over $n$ qubits.
  2. If for depth $d$, a random circuit ensemble is a $1$ design, then it is also a $1$ design at depth $d+1$ and beyond.

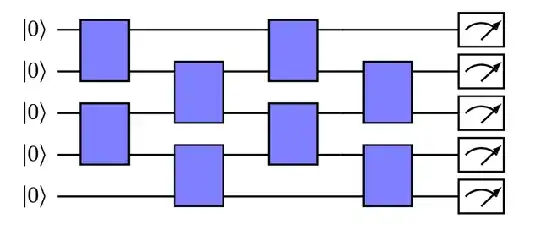
Now, consider the following random circuit ensemble, taken from Figure 1 (a) here.

enter image description here

As mentioned in the paper, each violet box is drawn independently from the Haar measure on $\mathbb{U}(4)$.

Now, consider a circuit constructed like this, whose depth is exactly $1$. That is, we start with the all zeros state, apply a random gate to each of the $n/2$ pairs of qubits, and then measure in the standard basis.

It is not hard to work out that the ensemble is a $1$ design.

However, I am not sure how to prove that the ensemble remains a $1$ design (or even an approximate $1$ design) when we increase the depth to $2$ and beyond. The calculations for the depth $1$ case do not immediately generalize.

What is going on here?

Note that it is known that such architectures become $2$ designs (and hence, $1$ designs too) after linear depth. However, I am interested in the behaviour in constant or $\log n$ depths.

Additionally, the fact that the depth $1$ case is a $1$ design seemed to rely heavily on the type of gate set chosen. What if we change the gate set to another universal gate set --- like all single qubit gates and the CNOT gate?

Does it still remain a $1$ design (or an approximate $1$ design) or is the gate set in question very special?

BlackHat18
  • 1,527
  • 9
  • 22

1 Answers1

4

To study unitary $t$-designs, we define the moment operator with respect to a probability measure $\nu$ as $$ M_t(\nu) := \int_{U(d)} U^{\otimes t} (\cdot) (U^{\otimes t})^\dagger d\nu(U) \simeq \int_{U(d)} (U \otimes \bar U)^{\otimes t} d\nu(U). $$ Often, designs are defined via subsets $D\subset U(d)$ endowed with some "canonical" measure. For instance, if $D$ is finite one usually takes the normalised counting measure which turns the above integral into a finite sum that averages over the elements in $D$.

Then, $\nu$ is a unitary $t$-design if and only if its moment operator agrees with the one of the Haar measure on the unitary group: $$ M_t(\nu) = M_t(\mu_\mathrm{Haar}). $$

If we consider random circuits, where we draw the first gate w.r.t to a measure $\nu_1$, the second gate w.r.t. $\nu_2$ and so on, the total distribution is given by a convolution of measures $$ \nu = \nu_1*\nu_2*\dots*\nu_k. $$ The respective moment operator factorises $$ M_t(\nu) = \int (U \otimes \bar U)^{\otimes t} d\nu(U) = (U_1\cdots U_k \otimes \bar U_1\cdots \bar U_k)^{\otimes t} d\nu_1(U_1)\cdots d\nu_k(U_k) \\ = M_t(\nu_1)\cdots M_t(\nu_k) $$

The brickwork circuits you're considering consist of two distinct layers, the even and odd ones, and we can write the total measure as $\nu = (\nu_\mathrm{even}*\nu_\mathrm{odd})^{*k}$ for $2k$ layers.

Now for your second question about alternate gate sets. I am assuming that you're asking specifically about 1-designs. Note that the Haar-random moment operator can be written as $$ M_1(\mu_\mathrm{Haar},U(d^n)) = \int_{U(d^n)} U(\cdot) U^\dagger d\mu_\mathrm{Haar}(U) = \mathrm{tr}(\cdot ) \frac{I}{d^n} = M_1(\mu_\mathrm{Haar}, U(d))^{\otimes n}, $$ i.e. it factorises. Hence, if we want to construct a unitary 1-design on $n$ qudits, it is sufficient to simply pick a 1-design on every qudit individually.

For instance, the Pauli/Weyl operators will do.

Markus Heinrich
  • 5,652
  • 11
  • 22