Using distinguishability of non-orthogonal states to create a cloning device

Question

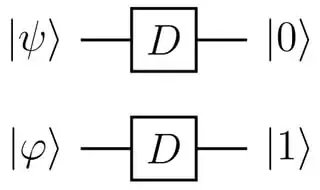
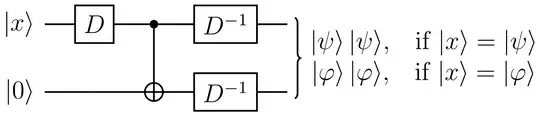
Consider the following problem from Nielsen and Chuang's Quantum Computation and Quantum Information:

Explain how a device which, upon input of one of two non-orthogonal quantum states $\left|\psi\right>$ or $\left|\phi\right>$ correctly identified the state, could be used to build a device which cloned the states $\left|\psi\right>$ and $\left|\phi\right>$, in violation of the no-cloning theorem. Conversely, explain how a device for cloning could be used to distinguish non-orthogonal quantum states.

I know that this problem has already been posted at least two times here and here, but I am not satisfied with the answers to the first part given there. As you can see, all answers to the first part basically tell you to use the device to distinguish between $\left|\psi\right>$ and $\left|\phi\right>$ and then just prepare an identical state. However, nowhere does this exercise say that we know how to prepare states $\left|\psi\right>$ and $\left|\phi\right>$. Moreover, preparing an identical state is not the same as cloning. A cloning device has to be able to replicate a state without having any prior knowledge about its "internal" structure. With this in mind, I am posting this problem once again.

Here is my attempt to address this problem. Let us say that we have two non-orthogonal states $\left|\psi\right>$ and $\left|\phi\right>$. We can measure $\left|\phi\right>$ in the basis of $\left|\psi\right>$, and feed the result to our magical device. Since $\left|\phi\right>$ is non-orthogonal to $\left|\psi\right>$, there is non-zero probability that measurement will give us another $\left|\psi\right>$. In this case the device will identify it as $\left|\psi\right>$, which means we have created a clone. If the measurement projects $\left|\phi\right>$ to some other state $\left|\psi'\right>$, orthogonal to $\left|\psi\right>$, then the device will not identify it as $\left|\psi\right>$, and we can repeat the process by measuring $\left|\psi'\right>$ again in the basis of $\left|\phi\right>$, which will create another state non-orthogonal to $\left|\psi\right>$.

This solution is also quite flimsy for the following reasons. First, I am not sure if an arbitrary unknown state can be used as a basis for measurement. Second, this solution never actually used the device to distinguish between $\left|\phi\right>$ and $\left|\psi\right>$. It only used it to distinguish between $\left|\psi\right>$ and not $\left|\psi\right>$, but it is unclear what happens if we try to feed a state other than $\left|\phi\right>$ and $\left|\psi\right>$ to the device, so this way was probably not implied by the authors of the exercise.

Any ideas?

Answer 1

I think you've maybe missed some of the reasoning in the premise.

If you are trying to clone an unknown qubit, but you know it to be one of two states $|\psi\rangle$ or $|\phi\rangle$, then the point is that you do know what $|\psi\rangle$ and $|\phi\rangle$ are. And, because we're assuming you can perfectly perform arbitrary unitaries (we don't care in this context about how long it might take), we can easily specify two unitaries which act as $$ U_1|0\rangle=|\psi\rangle,\qquad U_2|0\rangle=|\phi\rangle. $$
In fact, for this argument, I don't even have to talk quite so generically. I could be specific and say $|\psi\rangle=|0\rangle$ and $|\phi\rangle=|+\rangle$. So you definitely know how to make them.

Cloning is absolutely the case where you start from your unknown state $|\gamma\rangle$, and produce one (or more) copies $|\gamma\rangle|\gamma\rangle$. In this particular setting, we can produce as many copies as we want. The "internal" structure to which you are referring in this case is only the question of which of the two states it is, and not what those two possible states are.

Answer 2

I interpret this exercise as asking the following two question:

1. Given a quantum gate that can deterministically distinguish between $|\psi\rangle$ and $|\varphi\rangle$, construct a quantum circuit that can clone the states $|\psi\rangle$ and $|\varphi\rangle$.
2. Given a quantum gate that can clone both $|\psi\rangle$ and $|\varphi\rangle$, construct a quantum circuit that can distinguish the states $|\psi\rangle$ and $|\varphi\rangle$.

Creating a cloner from a distinguisher

When tackling the first part, we'll start by giving a precise representation to the quantum gate for distinguishing between $|\psi\rangle$ and $|\varphi\rangle$. We will denote this gate by $D$. It can be seen that the gate defined by the following two circuits satisfies the criteria for distinguishing.

Each of these two circuits represents two scalar equations, giving us four equations to uniquely determine the $2\times 2$ matrix representation of $D$. Let $$|\psi\rangle=a|0\rangle+b|1\rangle$$ $$|\varphi\rangle=c|0\rangle+d|1\rangle$$ where $a\overline{c}+b\overline{d}\neq0$, $a\overline{c}-b\overline{d}\neq0$, and $|a|^2+|b|^2=|c|^2+|d|^2=1$. These requirements on $a,b,c,d$ ensure that $|\psi\rangle$ and $|\phi\rangle$ are not orthogonal nor coincident and have probability amplitudes that sum to one. The circuits yield the following system of equations $$D_{11}a+D_{12}b=1$$ $$D_{21}a+D_{22}b=0$$ $$D_{11}c+D_{12}d=0$$ $$D_{21}c+D_{22}d=1$$ which has the solution $$D=\frac{1}{ad-bc}\begin{bmatrix} d & -c \\ -b & a \end{bmatrix}$$ Upon testing whether or not $D$ is unitary by checking if $D^\dagger D=I$, we immediately discover why such a gate cannot be made. $D^\dagger D=I$ if and only if $|\psi\rangle$ and $|\phi\rangle$ are orthogonal, since the off-diagonals of $D^\dagger D$ have $ac+bd$ as their numerators. Thus, when $|\psi\rangle$ and $|\phi\rangle$ are not orthogonal, $D$ is not unitary and therefore it is not a physical quantum gate. Since this question is non-physical in nature, due to breaking the laws of physics like the no-cloning theorem, we will suspend our disbelief and suppose that $D$ is unitary anyway. This will enable us to employ $D^{-1}=D^\dagger$ despite its numerical representation being unsolvable. We can now construct our cloning circuit. For $|x\rangle\in\{|\psi\rangle,|\varphi\rangle\}$ the following circuit will clone $|x\rangle$

When $|x\rangle$ passes through the $D$ gate, it will be transformed into $|0\rangle$ if $|x\rangle=|\psi\rangle$ and $|1\rangle$ if $|x\rangle=|\varphi\rangle$. The CNOT gate will then flip the second bit if $|x\rangle$ was originally $|\varphi\rangle$ and will keep it at $|0\rangle$ if $|x\rangle$ was originally $|\psi\rangle$. Thus, before the final $D^{-1}$ gates, we have the 2-qubit state $|0\rangle|0\rangle$ or $|1\rangle|1\rangle$. The $D^{-1}$ gates transform this into $|\psi\rangle|\psi\rangle$ or $|\varphi\rangle|\varphi\rangle$. Therefore, this circuit satisfies the criteria of being a cloner composed of distinguishing gates.

Creating a distinguisher from a cloner

I don't think this can be done with certainty. Please refer to the answer given here for an explanation of the best method for distinguishing.

Define gates to change basis to the coordinate systems mentioned in that answer ($\Psi=\{|\psi\rangle,|\psi'\rangle\}$ for $|\psi\rangle$ and $\Phi=\{|\varphi\rangle,|\varphi'\rangle\}$ for $|\varphi\rangle$). We can clone $2n$ copies of an input state, $|x\rangle$, and change basis, half into the $\Psi$ basis and half into the $\Phi$ basis. Performing measurements here will yield results of $|0\rangle$ when $|x\rangle$ collapses into $|\psi\rangle$ and $|\varphi\rangle$ respectively. We can then perform $\mathrm{OR}$ operations over all $n$ copies for each basis. Thus in our output, we will look to the two target bits that store the results of these $\mathrm{OR}$ operations. One result will be $|0\rangle$ if all measurements in the $\Psi$ basis collapsed to $|\psi\rangle$ and the other will be the same but for the $\Phi$ basis collapsing to $|\varphi\rangle$.

If we obtain one $|0\rangle$ and one $|1\rangle$, then we're good, and the basis that gave the $|0\rangle$ result tells us which state $|x\rangle\in\{|\psi\rangle,|\varphi\rangle\}$ was. If communication is noiseless, it should be impossible to get a $|11\rangle$ result, since $|x\rangle$ must be either $|\psi\rangle$ or $|\varphi\rangle$. If we get $|00\rangle$, then we have obtained the indeterminate result. This means that all our measurements were indicative of $|\psi\rangle$ and $|\varphi\rangle$ states and none yielded $|\psi'\rangle$ or $|\varphi'\rangle$. For large $n$, this should be fairly unlikely if the angle (on the Bloch sphere) between $|\psi\rangle$ and $|\varphi\rangle$ isn't terribly small.