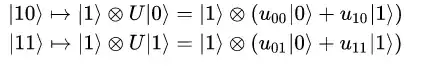Where exactly does entanglement appear in Shor's algorithm?

Question

One deals with the notion of superposition when studying Shor's algorithm, but how about entanglement? Where exactly does it appear in this particular circuit?

I assume it is not yet present in the initial state $\left|0\right>\left|0\right>$, but how about in further process, after applying Hadamard gates, the controlled-U gates and the inverse Fourier transform?

I understand that the first and second registers have to be entangled, otherwise, the final measurement on one of them wouldn't collapse the other one, which gives us the period (well, kind of, we need to use continuous fractions to infer it).

Answer 1

Your question contains the answer, as you mention the controlled-U gate which is an entangling gate. You will see in the page I linked, that the action of c-U on $|+\rangle|0\rangle$ for example can turn the state into one which cannot be written as a product:

$|+\rangle|0\rangle = \left( \frac{|0\rangle+|1\rangle}{\sqrt{2}} \right)\otimes |0\rangle = \left( \frac{|00\rangle+|10\rangle}{\sqrt{2}} \right)= \left( \frac{|00\rangle+|1\rangle U| 0\rangle}{\sqrt{2}} \right) = \left( \frac{|00\rangle+|1\rangle \left(u_{00}|0\rangle + u_{10}|1\rangle\right)}{\sqrt{2}} \right)$

In the last step, I used the definition of $U$ from the linked controlled-U description:

An example where this gate is entangling is where $u_{00}$ = 0 and $u_{10}=1$, which is just the $\rm{CNOT}$ gate. In that case we get $\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)$ which is the Bell state and is maximally entangled.

You may also be interested in this article on: "Entanglement and it's role in Shor's algorithm".