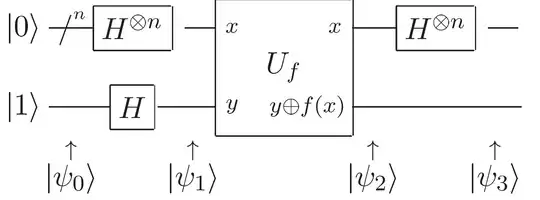
First of all, if we write down $\left|\psi_1\right\rangle$, we get:
$$\left|\psi_1\right\rangle=\frac{1}{\sqrt{2}^n}\sum_x|x\rangle\left[\frac{|0\rangle-|1\rangle}{\sqrt{2}}\right].$$
Applying $f$ on this state gives us:
$$\left|\psi_2\right\rangle=\frac{1}{\sqrt{2}^n}\sum_x|x\rangle\left[\frac{|f(x)\rangle-|1\oplus f(x)\rangle}{\sqrt{2}}\right].$$
Note that $f(x)$ is a bit. As such, $f(x)\oplus 1$ is actually $f(x)$ on which one applied a NOT gate. So, for a given $x$, if $f(x)=0$, then we can write:
$$|f(x)\rangle-|1\oplus f(x)\rangle = |0\rangle-|1\rangle$$
while we can write, if $f(x)=1$:
$$|f(x)\rangle-|1\oplus f(x)\rangle = |1\rangle-|0\rangle = -\left(|0\rangle-|1\rangle\right).$$
Thus, it is completely equivalent to write, in the general case:
$$|f(x)\rangle-|1\oplus f(x)\rangle = (-1)^{f(x)}\left(|0\rangle-|1\rangle\right).$$
Indeed, in the case $f(x)=0$, the $(-1)$ will disappear, while in the case $f(x)=1$, it will stay, just like in the two previous equations. This means that we can rewrite the state as:
$$\left|\psi_2\right\rangle=\frac{1}{\sqrt{2}^n}\sum_x|x\rangle(-1)^{f(x)}\left[\frac{|0\rangle-|1\rangle}{\sqrt{2}}\right]$$
which is the state described in Nielsen and Chuang.