If density matrices are linear operators, what vectors do they operate on?

Question

1. On page 73 of John Watrous' famous book, a quantum channel is defined as a linear map

$$\Phi: L(\mathcal{X})\rightarrow L(\mathcal{Y})$$

Now $L(\mathcal{X})$ stands for $L(\mathcal{X},\mathcal{X})$, which is itself a collection of all linear mappings $\mathcal{A}: \mathcal{X}\rightarrow \mathcal{X}$ (page-8).

2. As a physics student, when I look at some simple examples of a quantum channel, say a phase damping channel $\Phi_{PD}$, the way I look at it is that it takes my initial state $\rho_i$ at time $t_i$ to a final state $\rho_f$ at time $t_f$.

$$\Phi_{PD} [\rho_i] \rightarrow \rho_f$$

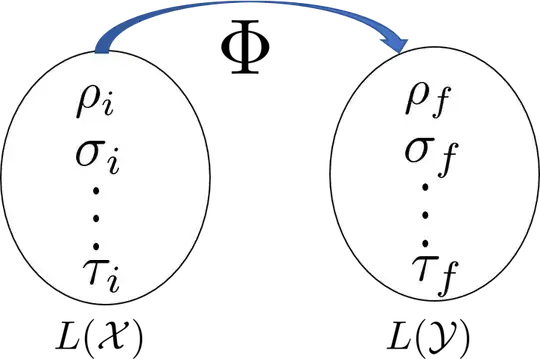
Trying to compare these two scenarios, it seems $\rho_i \in L(\mathcal{X})$ and $\rho_f \in L(\mathcal{Y})$. What happens to $\mathcal{A}$ here? What is exactly the one-to-one correspondence between 1 and 2?

Edit: I have tried to convey my query by a diagram in which the job of $\Phi$ is illustrated. I want to understand what is $\mathcal{A}$ in the following diagram:

Answer 1

1. The set $\mathrm L(\mathcal X)\equiv\mathrm L(\mathcal X,\mathcal X)$ is the set of linear maps from $\mathcal X$ to $\mathcal X$. In other words, $A\in\mathrm L(\mathcal X)$ iff $A$ is a linear function of the form $A:\mathcal X\to\mathcal X$.

2. Note that $\mathrm L(\mathcal X,\mathcal Y)$ is itself a vector space. That means you can have, for example, $\mathcal X\equiv \mathrm L(\mathcal Y,\mathcal Z)$ in the above. Quantum maps are examples of this: $\Phi\in\mathrm L(\mathrm L(\mathcal X),\mathrm L(\mathcal Y))$ means that $\Phi$ is a linear function $\Phi:\mathrm L(\mathcal X)\to\mathrm L(\mathcal Y)$. More explicitly, for any $\lambda,\mu\in\mathbb C$ (I'm assuming $\mathcal X,\mathcal Y$ to be complex vector spaces here) and $A,B\in\mathrm L(\mathcal X)$, you have $$\Phi(\lambda A+ \mu B) = \lambda \Phi(A)+\mu\Phi(B).$$ Note that in this, $A,B:\mathcal X\to\mathcal X$, meaning they are also linear functions, and thus for any $\alpha,\beta\in\mathbb C$ and $x,y\in\mathcal X$ you have $$A(\alpha x+\beta y)=\alpha A(x) + \beta A(y), \quad B(\alpha x+\beta y)=\alpha B(x) + \beta B(y).$$ To fix ideas, in the context of quantum information you typically have $A,B$ as density matrices of some quantum state, and $\lambda,\mu$ will be real scalars because $\lambda \rho$ is not a state if $\rho$ is a state and $\lambda\notin\mathbb R$.

3. Following the above discussion, an operator $A\in\mathrm L(\mathcal X)$ can be thought of as a function $\mathcal X\to\mathcal X$, or as a vector in $\mathrm L(\mathcal X)$. Both things are true and consistent with each other. Matrices are, in general, ways to represent linear operators, so whenever you work with a matrix, you are doing exactly this.