Why are there eight $T$ magic state and twelve $H$ magic states?

Question

I am learning magic state distillation.

We can define the following two states:

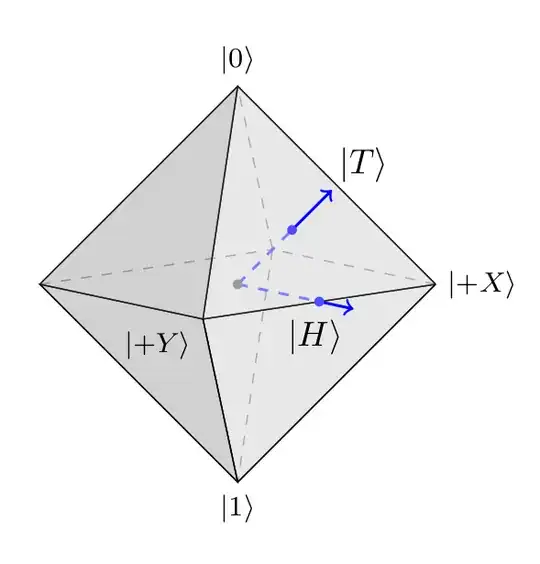
$$ |T\rangle \langle T | = \frac{1}{2}(I+\frac{1}{\sqrt{3}}(\sigma_x+\sigma_y+\sigma_z))$$ $$ |H\rangle \langle H | = \frac{1}{2}(I+\frac{1}{\sqrt{2}}(\sigma_x+\sigma_z))$$

From those states, we can define the $T$ and $H$-type magic states as respectively the set of states $\{ U |T \rangle\langle T| U^{\dagger}| U \in C_1\}$ and $\{ U |H \rangle\langle H| U^{\dagger}| U \in C_1\}$, where $C_1$ is the Clifford group.

In this paper, it is claimed that there are eight magic states of the $T$ type, and twelve of the $H$ type.

I could do some "brute force" calculation to check that with mathematica. But I wondered if there is a way to understand it easily ?

Initially I tried the following: if I act with Clifford element, each the Pauli matrices entering for instance for $|H\rangle \langle H | $ would be changed in another single qubit Pauli matrix (up to $\pm 1$ or $\pm i$) and I then simply have to count for all the possibilities. But it seems more complicated than that. Indeed, for instance $\sigma_x + \sigma_y$ cannot be changed to $\sigma_z + \sigma_z$ by acting with a Clifford element (the $|H\rangle \langle H|$ wouldn't be pure anymore which is absurd). Thus the counting seems more complicated because some combination are actually impossible to occur and it does not seem easy at first view to find which one. This is probably not doable without brute-force but as I am not sure (there is probably some smart way to show it), I am asking here.

Answer 1

It becomes very simple when you look at it in the Bloch representation

(Figure by me. Ref: Robustness of Magic and Symmetries of the Stabiliser Polytope)

The depicted octahedron is the polytope spanned by the 1-qubit stabiliser states (the Pauli eigenstates) and sits inside the Bloch sphere.

The Clifford group is exactly the symmetry group of the stabiliser polytope,* i.e. it is generated by $\pi/2$ rotations around the $X$, $Y$, and $Z$ axis.

You can see that the $|T\rangle$ state is normal to a facet of the stabiliser polytope. This is preserved under the Clifford orbit and since there are in total 8 facets, we have 8 $|T\rangle$ states.

$|H\rangle$ is normal to an edge. Through the Clifford action, you can reach any edge and there are in total 12 of them.

*It is the symmetry group within $\mathrm{SO}(3)$. Additionally, there are reflections, which come from an anti-unitary extension of the Clifford group. See App. C in Robustness of Magic and Symmetries of the Stabiliser Polytope.

Answer 2

Your reasoning is in the correct direction, but realize that $C_{1}$ permutes the $3$ Paulis, and adds a $\pm 1$ on any of the Paulis. See for instance Table 1 on page 20 of Entanglement in Graphstates. This is the explanation why $\sigma_{x} + \sigma_{y}$ cannot be transformed to $\sigma_{z} + \sigma_{z}$ - if $\sigma_{x}$ is already transformed to $\sigma_{z}$, $\sigma_{y}$ and $\sigma_{z}$ necessarily both need to become something different than $\sigma_{z}$.

Note, moreover, that there are no $\pm i$ phases - an easy way to see why this cannot be is that if $\sigma_{i}$ is Hermitian (which we know they are) then so must be $U \sigma_{i} U^{\dagger}$ - but then the 'output' cannot carry a phase $\pm i$, since any $\pm i \sigma_{j}$ is anti-Hermitian.

The $|T\rangle \langle T|$ state has all $3$ Paulis included. If you don't care about the phases, the conjugation with the Clifford can only permute these $3$ Paulis, which is essentially doing nothing, since $(\sigma_{x} + \sigma_{y} + \sigma_{z})$ sums to the same in any order that you sum the elements (i.e. Pauli operators are associative). Once you do include the phases, there's a $\pm 1$ option for every of three Paulis, for a total of $2^{3} = 8$ options.

The $|H\rangle \langle H|$ state has only two of three Paulis included. Hence, if you do not look at the phases, there are $3 \times 2$ options (three for the first Pauli, and two left for the second Pauli) - but you're counting twice too many due to, again, associativity$^{1}$. Essentially, you're counting the number of ways you can pick two elements of three elements in total, where you don't care about the order in which you pick them - that's the same as leaving one element out, out of the three elements - obviously there are three options for this. Each Pauli can again get a $\pm 1$ phase adding a factor of $2^{2}$, for a total of $3 \times 2^{2} = 12$ options.

$^{1}$ (e.g. $(\sigma_{x} + \sigma_{z})$ is the same as $H(\sigma_{x} + \sigma_{z})H^{\dagger}$).