In ZX-calculus, the $\pi$-copy rule is quite famous, and is used for instance here:
However, this paper never introduces this rule, and says that this set is enough to prove the Clifford completeness of the ZX calculus:
Is it just that they forgot it, or is this rule derivable from others?
It's indeed not, and so are other rules frequently used, like what we called Hopf law. These things were derived in the 2011 ZX-paper with Ross Duncan. Think of them as shortcuts. Many more of those have been derived by others and are frequently used. In our dodo book we have an entirely different rule taking care of red-green-phase interaction. This is really what a lot of maths is about: deriving results that simplify reasoning.
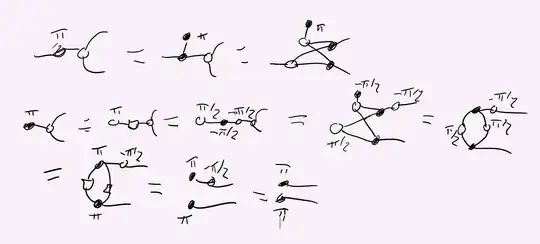
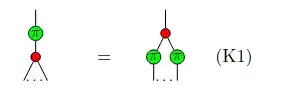
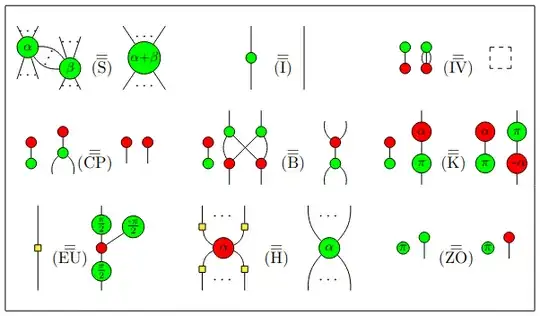
After asking on the Discord (thanks for pointing me to that Bob!), I got several proofs.
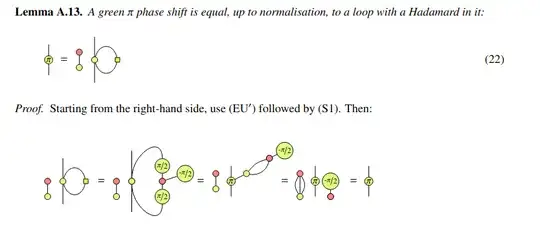
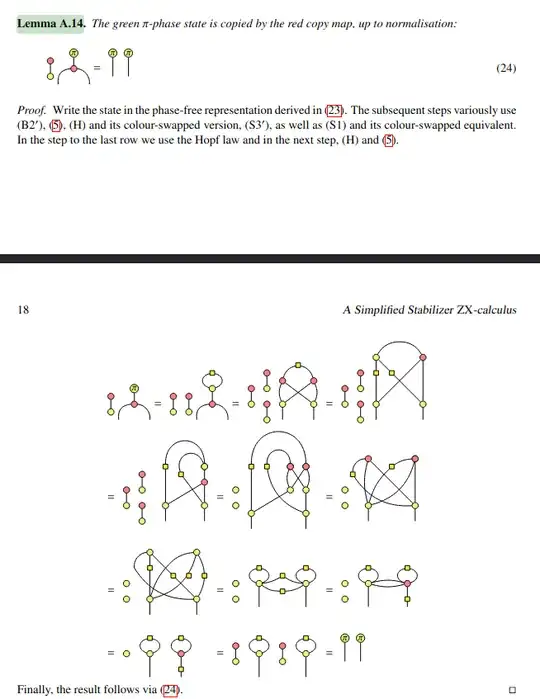
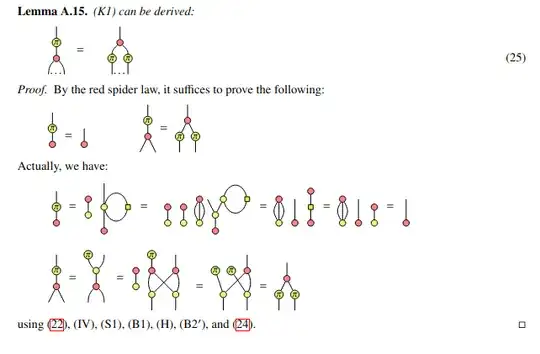
Lemma A.13, A.14 and A.15 of this paper, which contains also many interesting proofs. This method also works in the real stabiliser fragment, where Lemma A.13 is taken as a an axiom instead of the EU rule.
First, we derive the Y-state-identity, for instance given here in appendix A (I rewrote the proof with scalars):
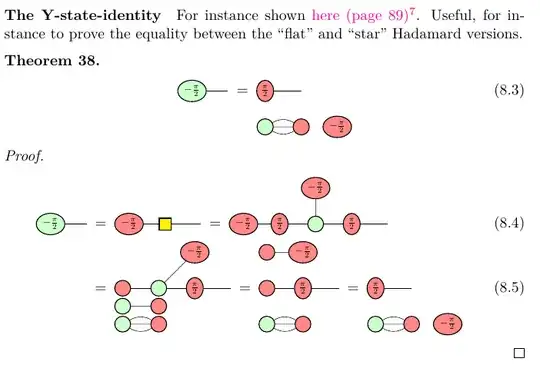
It is now trivial to derive the equivalence between the two forms of the Hadamard (it is also possible to show that the last form is true when inverting all angles by using the fact that $HH=I$):
Then, John was proposing this reduction (sorry, I've no time to write it down properly, so I shamefully copy/pasted his picture), where the Y-state identity is used in the last equation of the first line, and where the Hadamard identity is used right after, then it is the Hopf rule and the last equality can be proven using the K-rule + bialgebra + hopf (one may need also a proper analysis of scalars...):
