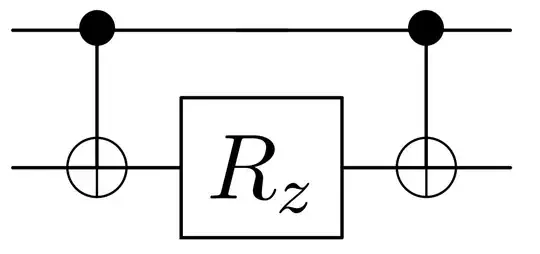
I'm trying to figure out the quantum circuit to simulate the time-evolution of a 2-qubit Hamiltonian $e^{iX_1\otimes X_2t}$, where $X$ is a Pauli gate. From this answer, the quantum circuit performs $e^{iZ_1\otimes Z_2t}$ could be constructed as an $R_z$ gate sandwiched by 2 controlled x gates. Can I replace $R_z$ by $R_x$ (and same goes for $R_y$) to simulate $e^{iX_1\otimes X_2t}$ and $e^{iY_1\otimes Y_2t}$? Thanks!
1 Answers
You can't just replace $R_z$ with $R_x$ - the $R_x$ would commute with the controlled-not, so the two controlled-nots cancel and all you get out is just the $R_x$.
The trick that you want to use instead is that $Ue^{-iHt}U^\dagger=e^{-iUHU^\dagger t}$. Now, we know that you can transform $Z\otimes Z$ into $X\otimes X$ using hadamards. So set $U$ to be the two-fold tensor product of Hadamards. Having said that, there are further circuit identities that you can use to simplify the circuit. You ultimately find that to get the $X\otimes X$ term, you need a circuit where you (i) replace the $R_z$ with $R_x$ and (ii) reverse the direction of the two controlled-nots.
You can follow a similar process to get $Y\otimes Y$ terms using $$ U=\frac12(Z+Y)\otimes(Z+Y), $$ but I'm not sure the circuit simplifies to the same extent.
Since you mention both $X\otimes X$ and $Y\otimes Y$ terms, I should point out that if the Hamiltonian that you actually want to simulate is $X\otimes X+Y\otimes Y$, you might be better off doing that directly rather than breaking it down into a pair of terms. What you need to think about is what is the unitary that diagonalises the term $X\otimes X+Y\otimes Y$, which is basically the inverse of the unitary that produces the Bell basis.
- 62,671
- 4
- 55
- 140