What is the basic hardware gate library in the IBM & google?

Question

I need to know what is the basic hardware gate library in hardware IBM and Google? I mean, which one of the gates can be implemented directly in the hardware. I would be very grateful if everyone helps me.

Answer 1

IBM

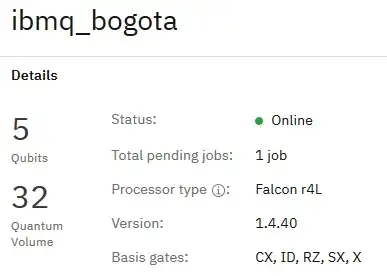
You can view the basis gates that supporting at the hardware level for IBM's hardware through your dashboard. All the devices with more than 1 qubit have the same set of basis gates $\{CX, ID, RZ, SX, X \}$. Below is a screenshot of a particular device named ibmq_bogota.

---

Google

From google's quantum computer datasheet and Cirq documentation here it seems like the google devices implement the following set of gates:

One qubit gate: $U3$ (general one-qubit gates pf any rotation), $X, Y, Z$.

Two qubit gates: Sycamore gate, which has the matrix representation as $\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & -i & 0 \\ 0 & -i & 0 & 0 \\ 0 & 0 & 0 & e^{-i\pi/8} \end{pmatrix}$

The $\sqrt{iSWAP}$ gate which has the matrix representation as $\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \frac{1}{\sqrt{2}} & \frac{i}{\sqrt{2}} & 0 \\ 0 & \frac{i}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}$

Other two qubit gate that being supported is the $CZ$ gate.

---

IonQ

The gates supported by the IonQ device are:

One qubit gates: $ GPI(\phi) = \begin{pmatrix} 0 & e^{-i\phi} \\ e^{i\phi} & 0\end{pmatrix}, GPI2(\phi) = \begin{pmatrix} 1 & -ie^{-i\phi} \\ -ie^{i\phi} & 1\end{pmatrix}, GZ(\theta) = \begin{pmatrix} e^{-i\theta/2} & 0 \\ 0 & e^{i\theta/2} \end{pmatrix} $

Two qubit gates: The Mølmer-Sørenson gate (MS): $\dfrac{1}{\sqrt{2}}\begin{pmatrix}1 & 0 & 0 & -i\\ 0 & 1 & -i & 0\\ 0 & -i & 1 & 0\\ -i & 0 & 0 & 1 \end{pmatrix}$

See this documentation by IonQ for more details.