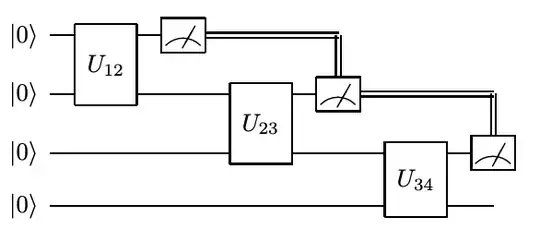
In this paper section 4.2 the author describes how to efficiently simulate linearly assembled quantum states. When describing the procedure to do so the author shows the following circuit:
The procedure for classic simulation is outlined is as follows
It is easy to use a classical computer to simulate such a circuit. First, we consider the result of applying $U_{12}$ to $|00\rangle$, and compute the probabilities for the measurement on qubit 1. We then sample from this distribution to produce a posterior state for qubit 2, which is used as an input for $U_{23}$. We then repeat this cycle of computing probabilities, sampling, and computing posterior states.
I was wondering if someone could further elaborate on this and fill in some blanks for me, for instance how is the posterior state produced? What exactly happens to that posterior state? Is there any way to prove that this simulation infact accurately describes the probabilities of our quantum circuit?