Complexity of $n$-Toffoli with phase difference

Question

I'm interested in the $n$-Toffoli gates with phase differences. I found a quadratic technique in section 7.2 of this paper.

Here's the front page of the paper.

Here's an image of the section that I'm referring to.

Does anyone know if there has been any improvement on the decomposition of the general n-qubits control X with phase differences in terms of elementary gates up to this day? Phase differences have to be consistent but not need fixing. Feedback is not allowed and no ancilla qubits are used.

And also what is the theoretical lower bound?

Answer 1

(This answer uses ancillae and feedback)

Does anyone know if there has been any improvement on the decomposition of the general n-qubits control X with phase differences in terms of elementary gates up to this day? [...] And also what is the theoretical lower bound?

About a week ago I would have told you it's probably not possible to do better than a T cost of $4n \pm O(1)$. But then, well...

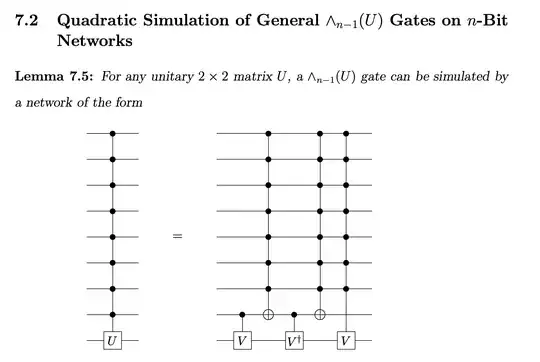
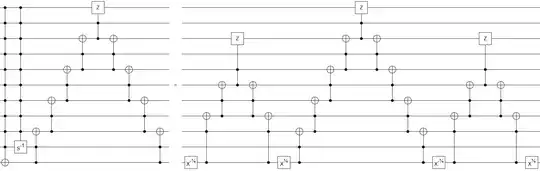
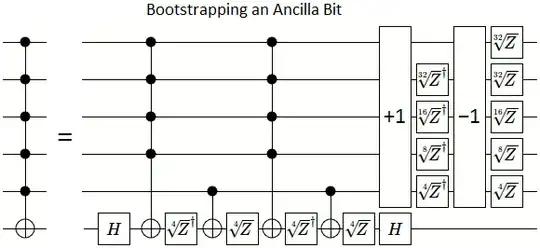
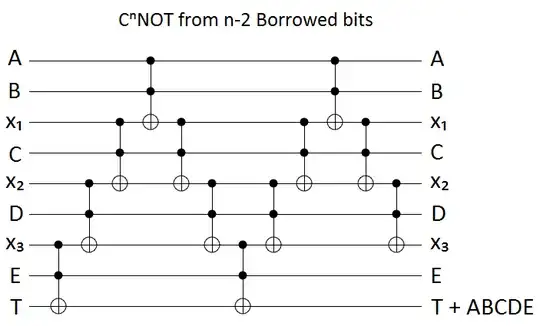
Here's a construction that reduces an $n$-control Toffoli into an $n-2$ control Toffoli, with a 50/50 chance of introducing heralded phase error on the controls. It uses 6 T gates, 1 ancilla, 12 stabilizer gates, and classical feedback.

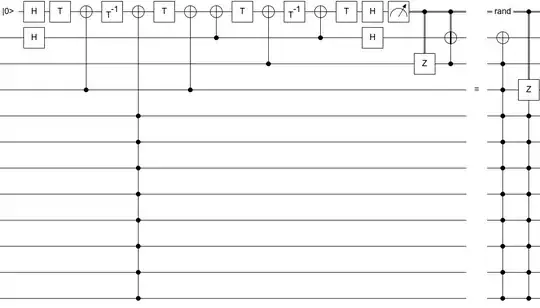
By iterating this construction, you can perform an $n$-control Toffoli with relative phase error using $3n$ T gates, $n/2$ ancillae, and $6n$ stabilizer gates.

The downside is that you will eventually need to correct the relative phase error, and this will cost you more than $n$ T gates so you ultimately come out behind vs just using ANDs to temporarily merge controls which has a total cost (including eventually fixing the phase error) of $4n$ T gates (that construction is explained in halving the cost of quantum addition).

Answer 2

Feedback is not allowed and no ancilla qubits are used.

Here's a relative-phase-error no-ancilla $C^n X$ construction with a T count of $12n \pm O(1)$.

I think it's easiest to understand as $3n \pm O(1)$ Toffoli gates with $O(1)$ other gates:

(Verification circuit in Quirk)

(The left hand side might not look like it only has relative phase error, but you can propagate the CCZ out of the Toffolis creating a more complicated looking phase error, and then all the Toffolis cancel out.)

The basic ideas in this construction are:

1. Start with the bootstrap ancilla circuit, but throw out the increments and phase gates on the controls since those are just to correct relative phase error. Also, instead of dividing the controls into two groups of wildly mismatched sizes, divide them into two evenly sized groups.

   

2. Each control group must control an X gate in two places in the circuit. Use the n-borrowed-ancilla $C^n X$, but conjugate the borrowed ancilla with Hadamards. This switches the direction of the Toffolis, and means that leaving out the "second mountain" in the construction that does not touch the target results in phase error instead of permutation error. We're fine with phase error, so leave out the second mountain.

   

3. Because the Toffolis all come in matched pairs, the mountain phase error from leaving out a moutain is free to commute across the circuit. And because the control group X gates each occur twice, this makes the mountain phase error all cancel out.

4. One of the control group Xs is next to a hadamard on the side of the circuit. It's actually a phase correction. Turn it into phase error by moving it to the left hand side of the equality.

5. Propagate the target Hadamard across the circuit, which ultimately makes it look simpler.

6. When decomposing the Toffolis into Clifford+T, you will want to use the 4T decomposition that has a phase kickback on the controls. Because the Toffolis in each mountain come in matched pairs whose controls are applied to the same computational basis states, the phase kickback from one member of the pair can be cancelled against the kickback from the other.