Cascade/Feedforward quantum circuits

Question

I would like to know if it is possible implement the following situation in Qiskit (either using the simulators or real quantum computers).

Consider this illustrative toy example:

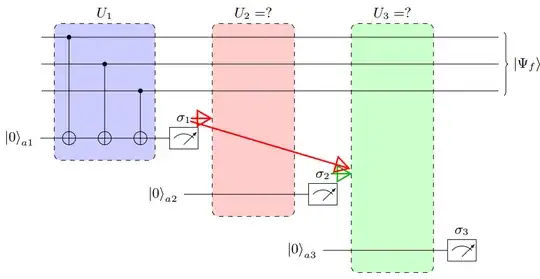
The arrows illustrate that the outcomes $\{\sigma_1,...,\sigma_i\}$ determine the unitaries $U_j$ for $j=i+1,...,n$. That is, the idea is that the unitary $U_2$ can only be determined once the outcome $\sigma_1$ is known, then the unitary $U_3$ can be determined once $\sigma_1$ and $\sigma_2$ are known, and so on and so forth as we move along the circuit.

The main idea and difficulty is precisely that we do not know the unitaries a priori and need to calculate them from the previous outcomes. (Note that determining all the possible unitary sequences before we start the computation would mean $2^n$ possible sequences for a computation with $n$ layers.)

So basically, I need Qiskit to run the blue box, do the first measurement and stay in "stand-by" (so to speak) while I determine what $U_2$ is. Once I have that information I would have to append $U_2$ to the previous circuit and execute this new portion of the circuit alone (i.e. without running the previous one again!). (If Qiskit re-executes the first block again, it might get the wrong outcome for $\sigma_1$ and everything will be ruined). Is this possible at all? If not: (i) what is the next best thing? and (ii) is there a prediction for when such functionality will be available and in which shape?

Thank you all!

---

EDIT: I seem to be looking for this: https://www.ibm.com/blogs/research/2021/02/quantum-phase-estimation/ ("dynamic quantum circuits"). There is also the arxiv pre-print reporting this: https://arxiv.org/abs/2102.01682. Now, I need only understand if this is a functionality that is accessible to general IBMQ users like myself, or if it is still to be made available.

Particularly, what I want is what the authors call "real-time compute" or "classical real-time logic". Because what I want to write is an algorithm that requires a dynamic circuit, not a static one.

Answer 1

I think the concept you are searching for is classically controlled gate, also known as conditional gate.

A conditional gate only has an effect if a classical value matches a predefine result. In your case, $U2$ is conditioned by $\sigma_1$, for example.

You can model that in Qiskit in the following way.

First, define your $U$s

from qiskit import QuantumCircuit
U1 = QuantumCircuit(4, name="U1")
# ... your U1 here
U1.cx(0, 3)
U1.cx(1, 3)
U1.cx(2, 3)
U2 = QuantumCircuit(8, name="U2")
... your U2 here
U3 = QuantumCircuit(12, name="U3")
... your U3 here

Then, compose your circuit. Pay special attention to U2 and U3, where the c_if method makes them classically controlled:

from qiskit import ClassicalRegister, QuantumRegister
psi = QuantumRegister(12, name="psi")
sigma_1 = ClassicalRegister(1, name="sigma_1")
sigma_2 = ClassicalRegister(1, name="sigma_2")
circuit = QuantumCircuit(psi, sigma_1, sigma_2)
circuit.append(U1.to_gate(), range(4))
circuit.measure(3, 0)
circuit.append(U2.to_gate().c_if(sigma_1, 1), range(8))
circuit.measure(7, 1)
circuit.append(U3.to_gate().c_if(sigma_2, 1), range(12))
print(circuit)

           ┌─────┐   ┌─────┐   ┌──────┐
    psi_0: ┤0    ├───┤0    ├───┤0     ├
           │     │   │     │   │      │
    psi_1: ┤1    ├───┤1    ├───┤1     ├
           │  U1 │   │     │   │      │
    psi_2: ┤2    ├───┤2    ├───┤2     ├
           │     │┌─┐│     │   │      │
    psi_3: ┤3    ├┤M├┤3    ├───┤3     ├
           └─────┘└╥┘│  U2 │   │      │
    psi_4: ────────╫─┤4    ├───┤4     ├
                   ║ │     │   │      │
    psi_5: ────────╫─┤5    ├───┤5     ├
                   ║ │     │   │   U3 │
    psi_6: ────────╫─┤6    ├───┤6     ├
                   ║ │     │┌─┐│      │
    psi_7: ────────╫─┤7    ├┤M├┤7     ├
                   ║ └──╥──┘└╥┘│      │
    psi_8: ────────╫────╫────╫─┤8     ├
                   ║    ║    ║ │      │
    psi_9: ────────╫────╫────╫─┤9     ├
                   ║    ║    ║ │      │
   psi_10: ────────╫────╫────╫─┤10    ├
                   ║    ║    ║ │      │
   psi_11: ────────╫────╫────╫─┤11    ├
                   ║ ┌──╨──┐ ║ └──╥───┘
sigma_1: 1/════════╩═╡ = 1 ╞═╬════╬════
                   0 └─────┘ ║ ┌──╨──┐ 
sigma_2: 1/══════════════════╩═╡ = 1 ╞═
                             0 └─────┘ 

Notice that U2 is executed only if the value in sigma_1 is 1. Similarly, U3 has effect if sigma_2 is 1.

Answer 2

IBM's Development Roadmap indicates that dynamic quantum circuits will be available by the end of 2022. See here:

https://www.ibm.com/blogs/research/2021/02/quantum-development-roadmap/