Can Dirac notation be used with 2 or more gates?
I've been trying to do the math with the $X$ and $Z$ ($X\otimes Z$) gates but I'm not getting the answer I should. In fact, the answer makes no sense. I'm new, so I'm trying to understand whether or not this notation will work mathematically when combining gates.
It works out fine when using matrix math, so I'm wondering if something like this is a limitation of Dirac notation.
$X \otimes Z = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} = \begin{pmatrix} 0 \cdot \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} & 1\cdot \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}\\ 1 \cdot \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} & 0 \cdot \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix}$
Note that here, $X \otimes Z$ acts on a two qubits system. For instance, if your two qubits is in the state $|\psi \rangle = |10\rangle = |1\rangle \otimes |0\rangle $ then $$(X \otimes Z) |\psi \rangle = \big(X \otimes Z \big) (|1\rangle \otimes |0\rangle) = X|1\rangle \otimes Z|0\rangle = |0\rangle \otimes |0\rangle =|00\rangle $$
This is the same if you have done the matrix multiplication, by first notice that $$|10\rangle = |1\rangle \otimes |0\rangle= \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix}= \begin{pmatrix}0 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ 1 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{pmatrix}= \begin{pmatrix}0\\ 0\\ 1\\ 0 \end{pmatrix}$$ then $$(X \otimes Z) |\psi \rangle = \begin{pmatrix} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0 \end{pmatrix} \begin{pmatrix}0\\ 0\\ 1\\ 0 \end{pmatrix} = \begin{pmatrix}1\\ 0\\ 0\\ 0 \end{pmatrix} = |00\rangle$$
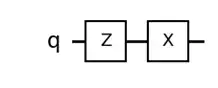
How this would appear on the quantum circuit is as follow:
Now, if you consider $XZ$, this is not the same as $X \otimes Z$ as the other answer by Hasan iqbal mentioned. This is just regular matrix multiplication. That is,
$$ X Z = X \cdot Z = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix} \cdot\begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix} = \begin{pmatrix} 0 & -1\\ 1 & 0\end{pmatrix} $$
This is a $2 \times 2$ matrix, and hence it acts only on a single qubit. So suppose you single qubit system is in the state $|\psi \rangle = |0 \rangle$. Then what this does is as follow:
$$ (XZ) |0 \rangle = X (Z|0 \rangle) = X(|0\rangle) = |1\rangle $$
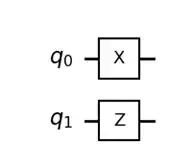
How this would appear on the quantum circuit is as follow:
Dirac notations, as far as I have seen, concerns quantum states (kets) and their complex conjugates (bras). For gates, you could simply use the capitalized letter that represents the particular gate. For example, $H$ for Hadamard gate, $X$ for bit flip, and so on. Please note that, when you apply two quantum gates on the same quantum state, the notation looks like the following. If you use $Z$ and $X$ on some single qubit quantum state $|\psi\rangle$, then it should read $ZX |\psi\rangle$, not $(Z \otimes X) |\psi\rangle$. The $\otimes$ sign means a tensor product.
