Quantum parallelism and Deutsch's algorithm - what is $U_f$ really?

Question

I'm trying to understand quantum parallelism ideas leading the Deutsch's algorithm. The circuit in question is

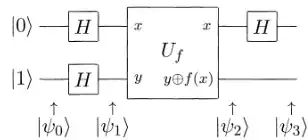
I understand that we end up with $$|\psi_3 \rangle = \pm | f(0) \oplus f(1) \rangle \left[ \frac{|0 \rangle - |1 \rangle }{\sqrt{2} } \right].$$ Then by measuring the first qubit we can determine $f(0) \oplus f(1),$ and the claim is that we have thus determined a global property of $f(x),$ namely $f(0) \oplus f(1),$ using only one evaluation of $f(x)$.

I have three questions:

1. Where does that single evaluation of $f(x)$ actually occur? Is it in the construction of $U_f$?
2. What is $U_f$ in this case? I realize it depends on $f$, but how can we build it using at most one evaluation of $f$?
3. In the circuit above, the $x$ input to $U_f$ is $(|0\rangle + |1 \rangle)/\sqrt{2})$. What does it mean to apply (classical) $f$ to this $x$?

I realize all 3 of these questions are probably tied up somehow.

Answer 1

Where does that single evaluation of $f(x)$ actually occur? Is it in the construction of $U_f$?

$U_f$ is an implementation of $f$ in quantum gates. The evaluation of $f$ occurs in the course of applying the gates making up $U_f$ to the qubits.

What is $U_f$ in this case? I realize it depends on $f$, but how can we build it using at most one evaluation of $f$?

You don't evaluate $f$ when building $U_f$, if by building it you mean determining what primitive gates make it up.

You could imagine that $f(x)$ is the first bit of the SHA-256 hash of $x$. In that case, $U_f$ would be a reversible circuit computing a SHA-256 hash. This might require, say, 100,000 primitive gates. Ultimately, there are only 4 functions that $f$ could be, but determining which of those four functions it is would require around 200,000 primitive operations. Determining $f(0)$ or $f(1)$ alone would require around 100,000 operations. Classically, determining $f(0)\oplus f(1)$ would require around 200,000 operations, but with Deutsch's algorithm you can find it in 100,000.

In the circuit above, the $x$ input to $U_f$ is $(|0\rangle + |1 \rangle)/\sqrt{2})$. What does it mean to apply (classical) $f$ to this $x$?

It doesn't mean anything to apply $f$ to it, but it means something to apply $U_f$ to it. By definition $U_f$ takes $|x\rangle|y\rangle$ to $|x\rangle|y\oplus f(x)\rangle$ for $x,y\in\{0,1\}$. This definition only covers four inputs, but adding the requirement that $U_f$ be linear completely fixes $U_f$. For example, you must have $$U_f\,(|0\rangle{+}|1\rangle)\,|0\rangle = U_f|0\rangle|0\rangle+U_f|1\rangle|0\rangle = |0\rangle|f(0)\rangle+|1\rangle|f(1)\rangle$$ (times $1/\sqrt2$).