I am using Jupyter Notebook with Qiskit.
I have created a program that can add two 3-bit numbers together. When I simulate this program on a qasm_simulator it works as expected and I can add any two 3-bit numbers together such as: $011 + 110 = 1000$
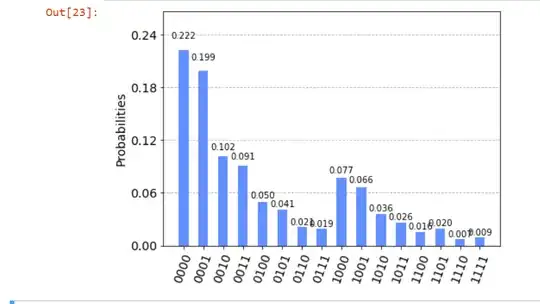
However, when I try to get the result on real quantum hardware (IBMQ) it gets very unexpected results as seen below.
I know there will obviously be noise when using the quantum hardware but the results aren't even close to what they should be, does anyone know why?
My code:
%matplotlib inline
# Importing standard Qiskit libraries
from qiskit import QuantumRegister
from qiskit import ClassicalRegister
from qiskit import QuantumCircuit, execute, Aer, IBMQ
from qiskit.compiler import transpile, assemble
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from ibm_quantum_widgets import *
from qiskit.tools.monitor import job_monitor
from qiskit.providers.ibmq import least_busy
Loading IBM Q account(s)
provider = IBMQ.load_account()
Create COUT sub-routine
q0 = QuantumRegister(1) # First number
q1 = QuantumRegister(1) # Second number, then sum
q2 = QuantumRegister(1) # Carry bit i
q3 = QuantumRegister(1) # Carry bits i+1
Build a COUT sub-circuit
COUT_qr = QuantumRegister(4)
COUT = QuantumCircuit(q0,q1,q2,q3,name='COUT')
COUT.ccx(q1[0],q2[0],q3[0])
COUT.cx(q1[0],q2[0])
COUT.ccx(q0[0],q2[0],q3[0])
convert to a gate
COUT_inst = COUT.to_instruction()
reverse COUT sub-routine
q0 = QuantumRegister(1) # First number
q1 = QuantumRegister(1) # Second number, then sum
q2 = QuantumRegister(1) # Carry bit i
q3 = QuantumRegister(1) # Carry bits i+1
Build a COUT sub-circuit
reverseCOUT = QuantumCircuit(q0,q1,q2,q3,name='reverseCOUT')
reverseCOUT.ccx(q0[0],q2[0],q3[0])
reverseCOUT.cx(q1[0],q2[0])
reverseCOUT.ccx(q1[0],q2[0],q3[0])
convert to a gate
reverseCOUT_inst = reverseCOUT.to_instruction()
Create SUM sub-routine
q0 = QuantumRegister(1) # First number
q1 = QuantumRegister(1) # Second number, then sum
q2 = QuantumRegister(1) # Carry bit i
Build a COUT sub-circuit
SUM = QuantumCircuit(q0,q1,q2,name='SUM')
SUM.cx(q0[0],q2[0])
SUM.cx(q1[0],q2[0])
convert to a gate
SUM_inst = SUM.to_instruction()
n is the length of the qubits you are adding together
n = 3
a = QuantumRegister(n,'a') # First number
b = QuantumRegister(n+1,'b') # Second number, then sum
c = QuantumRegister(n,'c') # Carry bits
cl = ClassicalRegister(n+1) # Classical output
Combining all of them into one quantum circuit
qc = QuantumCircuit(a, b, c, cl)
initialise numbers:
qc.x(0)
qc.x(1)
#qc.x(2)
qc.x(3)
#qc.x(4)
qc.x(5)
Create the circuit to add two 3-bit numbers
COUT
qc.append(COUT,[c[0],a[0],b[0],c[1]])
qc.barrier()
COUT
qc.append(COUT,[c[1],a[1],b[1],c[2]])
qc.barrier()
COUT
qc.append(COUT,[c[2],a[2],b[2],b[3]])
qc.barrier()
qc.cx(c[2],b[2])
qc.barrier()
reverse COUT
qc.append(reverseCOUT,[c[1],a[1],b[1],c[2]])
qc.barrier()
SUM
qc.append(SUM,[c[1],a[1],b[1]])
qc.barrier()
reverse COUT
qc.append(reverseCOUT,[c[0],a[0],b[0],c[1]])
qc.barrier()
SUM
qc.append(SUM,[c[0],a[0],b[0]])
qc.barrier()
Measure qubits and store results in classical register cl
for i in range(3+1):
qc.measure(b[i], cl[i])
Run the experimient 1024 times and get stats
counts = execute(qc,Aer.get_backend('qasm_simulator')).result().get_counts()
plot_histogram(counts)
Run on Quantum Hardware
provider = IBMQ.get_provider(hub='ibm-q')
backend = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 10
and not x.configuration().simulator
and x.status().operational==True))
print("least busy backend: ", backend)
Run it
shots = 2048
transpiled_qc = transpile(qc, backend, optimization_level=3)
qobj = assemble(transpiled_qc, shots=shots)
job = backend.run(qobj)
job_monitor(job)
Plot results
counts = job.result().get_counts()
plot_histogram(counts)