I'm self-studying quantum computing and have gone through the Wikipedia article on the Berstein-Vazirani algorithm and believe that I understand it. I'm looking to verify my understanding and hope that someone could help me.
If I have an 8 bit secret of all 0s, would the oracle just be nothing? Alternatively, if it was all 1s, would my oracle CNOT each input with the output qubit?
Yes, this is because the initial state will be starting as $|\psi_{init} \rangle = |000\cdots0\rangle = |0\rangle^{\otimes 8} $. Then you apply a layer of Hadamard gates, follow by the Oracle operation, then another layer of Hadamard gates, then finally the state of the 8 qubits of interest. Because the secret bitstring you have in mind are all $0$s, the Oracle would be nothing since this will allow the two layer of the Hadamard gates cancel each other out and keeping the state as $|\psi \rangle = |0\rangle^{\otimes 8}$. Now, upon measurement, you will extract out this very state... which is the secret bitstring you are interested in finding.
If your secret bitstring is all 1's then you would want your final state to be $|\psi\rangle = |1\rangle^{\otimes 8}$. To do this, we can use something called phase kickback. The idea is simple but clever. First notice the following:
This tells us, that if we want all $1$s then we will apply CNOT gates to each of the 8 qubits in your state to the ancilla qubit (which is in the state $\dfrac{|0\rangle - |1\rangle}{\sqrt{2}}$, which is created by apply $X$ gate follow by Hadamard gate) between the two layers of the Hadamard gates. Thus you will have something like this:
Measuring this will return you the state of all 1's.
With the Quantum Oracle $|x \rangle \xrightarrow{f_s} (-1)^{s\cdot x} |x \rangle$ (between the Hadamard sandwich) for the BV algorithm, with ($n$-bit) input secret bits $s$, here is what it does:
$|00\dots 0\rangle \xrightarrow{H^{\otimes n}} \frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} |x\rangle \xrightarrow{f_s} \frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} (-1)^{s\cdot x}|x\rangle \xrightarrow{H^{\otimes n}} |s\rangle$
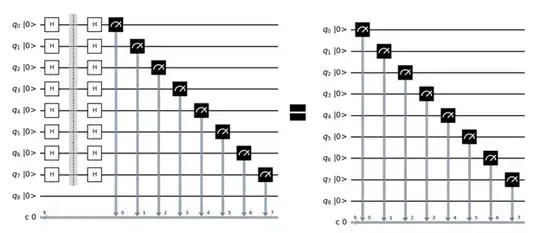
When $s=00\ldots0$, $(-1)^{s.x}=(-1)^0=1$, s.t. the orale $f_s$ become an identity operator, as can be seen from above:
$\frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} |x\rangle \xrightarrow{f_\textbf{0}} \frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} (-1)^{\textbf{0}\cdot x}|x\rangle$,
i.e.,
$\frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} |x\rangle \xrightarrow{f_\textbf{0}} \frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} |x\rangle$,
so that the oracle is an identity mapping (transformation) and it has to do nothing.
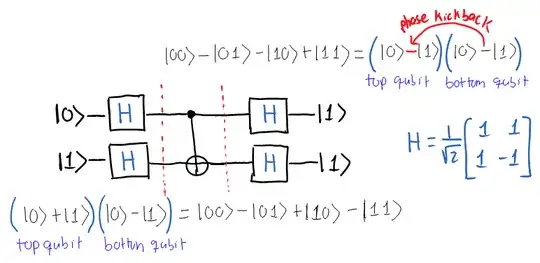
We need to have a $CNOT$ gate whenever there is a $1$ bit in the secret bits in the Oracle, in order to introduce phase-kickback at the query bits, but don't have to do anything where the secret bit is $0$, which can be seen from below.
$|0\rangle \xrightarrow{H} |+\rangle$
phase kickback: $|+ \rangle \otimes |- \rangle \xrightarrow{CNOT} |- \rangle \otimes |-\rangle$, with $|+\rangle$ as the control qubit
$|-\rangle \xrightarrow{H} |1\rangle$
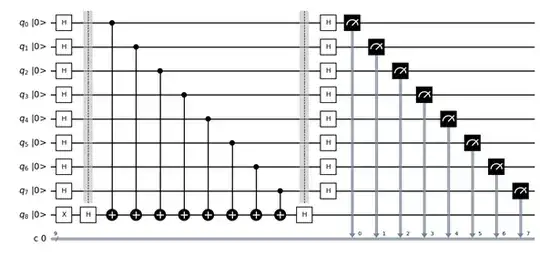
Hence, when $s=111\ldots 1$, we have the oracle as
$\frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} |x\rangle \xrightarrow{f_\textbf{1}} \frac{1}{\sqrt{2^n}} \sum\limits_{x\in \{0,1\}^n} (-1)^{\textbf{1}\cdot x}|x\rangle$,
and we need to have $CNOT$ gates for all the secret bits in the oracle.