Question on qiskit.circuit.library.PiecewiseChebyshev Qiskit circuit library

Question

This question follows the post https://quantumcomputing.stackexchange.com/posts/15070/.

I am working on an implementation of HHL algorithm, to do so, I need to map $|\lambda\rangle\mapsto |\arcsin(\frac{C}{\lambda})\rangle$, where $|\arcsin(\frac{C}{\lambda})\rangle$ is a binary representation $\arcsin(\frac{C}{\lambda})$ with $m$ qubits.

Recently, a circuit implementing a Piecewise Chebyshev approximation of a given function $f$ was implemented in Qiskit, documentation can be found here : https://qiskit.org/documentation/stubs/qiskit.circuit.library.PiecewiseChebyshev.html#qiskit-circuit-library-piecewisechebyshev.

I was working on the given example:

import numpy as np
from qiskit import QuantumCircuit
from qiskit.circuit.library.arithmetic.piecewise_chebyshev import PiecewiseChebyshev
f_x, degree, breakpoints, num_state_qubits = lambda x: 0, 2, None, 2
pw_approximation = PiecewiseChebyshev(f_x, degree, breakpoints, num_state_qubits)
pw_approximation._build()
qc = QuantumCircuit(pw_approximation.num_qubits)
qc.h(list(range(num_state_qubits)))
qc.append(pw_approximation.to_instruction(), qc.qubits)
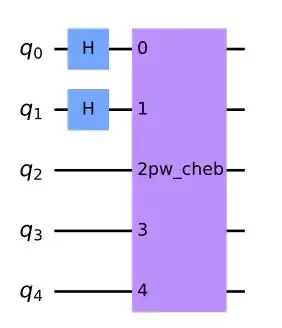
qc.draw(output='mpl')

which should implement a piecewise approximation of the zero function on two qubits ... We can take a look of what the circuit looks like:

the first and second qubits are state qubits and I guess that the three others are ancillary qubits.

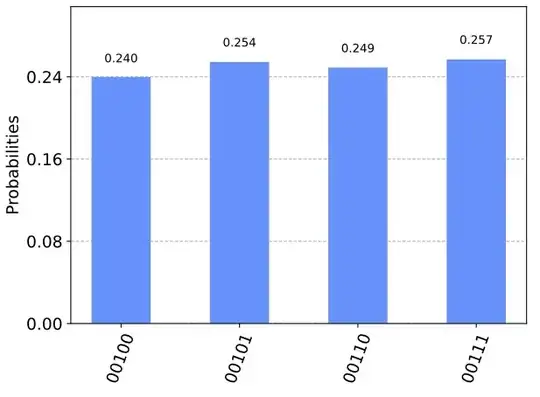
The initial state of the system is set to $\frac{1}{2} (|00\rangle+|01\rangle+|10\rangle+|11\rangle)$ so we may look at all possible results of the approximation.

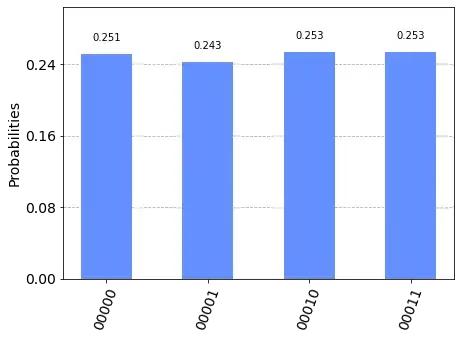
But while looking at measurements of the output qubits, I am facing weird results:

The third qubit is set to one, while the two first are unchanged. I tried a lot of different functions to understand how one can interpret the resulting qubits, but I still cannot figure out what the circuit does. Does anyone have an idea ?

Answer 1

The source of the problem was numpy.polynomial.chebyshev.interpolate, which is used to approximate the input function but raises problems when approximating a constant function.

The code in Qiskit has been changed adding a special case for such functions and explaining how constant functions should be declared, i.e. as f_x = constant rather than with the lambda declaration.

The updated code now performs as expected:

import numpy as np
from qiskit import *
from qiskit.visualization import plot_histogram
from qiskit.circuit.library.arithmetic.piecewise_chebyshev import PiecewiseChebyshev
f_x, degree, breakpoints, num_state_qubits = 0, 1, [0], 2
pw_approximation = PiecewiseChebyshev(f_x, degree, breakpoints, num_state_qubits)
pw_approximation._build()
qc = QuantumCircuit(pw_approximation.num_qubits, pw_approximation.num_qubits)
qc.h(list(range(num_state_qubits)))
qc.append(pw_approximation.to_instruction(), qc.qubits)
qc.measure(list(range(pw_approximation.num_qubits)), list(range(pw_approximation.num_qubits)))
qc.draw(output='mpl')

backend = BasicAer.get_backend('qasm_simulator') # the device to run on
result = execute(qc, backend, shots=10000).result()
counts  = result.get_counts(qc)
plot_histogram(counts)

And here is the link to the PR in case you want to check its status.

Regarding the operation $f(x)|0>\mapsto |f(x)>$, it is not supported in Qiskit yet but here is the relevant literature.

Answer 2

Since the PiecewiseChebyshev object implements the transformation $U |x\rangle |0\rangle \to |x\rangle \Big(\cos(f(x))|0\rangle + \sin(f(x))|1\rangle\Big)$, you need to apply amplitude estimation process in order to retrieve the value $\sin(f(x))$ into some $m$-qubit quantum register. You can of course define $f$ such that the $\sin$ function disappear.

I have tried with $f = \arcsin \sqrt{x / 2^m}$ so that I can immediately check if the circuit works: if I encode as input the $n$-qubit state $|i\rangle$ then I will read in the output $m$-qubit quantum register the number $i/2^m$:

from qiskit.circuit.library import PiecewiseChebyshev 
from qiskit import *
from qiskit.algorithms import AmplitudeEstimation, EstimationProblem, AmplitudeEstimationResult
from qiskit.utils import QuantumInstance
import numpy as np
from qiskit.extensions.quantum_initializer.initializer import Initialize
def create_state_preparation_for_arcsin_sqrt(N, number):
    """N: input bits
       number: 2**N elements vectors whose only non zero component is the i-th one, and number represents |i> vector
    """
if len(number) != 2**N:
    raise ValueError("Number must be a 2**N elements vectors")

func = lambda x: np.arcsin(np.sqrt(x / 2 ** N)) # The function to be implemented
degree = 5 # The degree of Chebyshev polynomials. Use higher degree for better approximation
breakpoints = [0, 2**N-1]
pw_approx = PiecewiseChebyshev(func, degree, breakpoints, N)
pw_approx._build()

qr_state = QuantumRegister(N, "state")
qr_output = QuantumRegister(1, "output")
qr_aux = QuantumRegister(pw_approx.num_ancillas, "aux")

qc = QuantumCircuit(N + 1 + pw_approx.num_ancillas)
gate = Initialize(number).gates_to_uncompute().inverse()
qc.append(gate, range(N))
qc.append(pw_approx.to_instruction(), range(N+1+pw_approx.num_ancillas))

qc2 = transpile(qc, basis_gates=["u3", "cx"])
return qc2, [N]


N = 3
number = np.array([0] * (2**3))
number[3] = 1
state_preparation, objective_qubits = create_state_preparation_for_arcsin_sqrt(3, number)
backend = Aer.get_backend('qasm_simulator', shots=10000)
qinstance = QuantumInstance(backend, seed_simulator=2, seed_transpiler=2)
m = 4
problem = EstimationProblem(state_preparation=state_preparation, objective_qubits=objective_qubits)
ae = AmplitudeEstimation(num_eval_qubits=m, quantum_instance=qinstance)
result = ae.estimate(problem)
print('Grid-based estimate:', result.estimation)
print('Improved continuous estimate:', result.mle)

Once you have defined the AmplitudeEstimation object correctly you can append the corresponding circuit using

ae_circuit = ae.construct_circuit(estimation_problem=problem)

and use it inside your workflow. However, it seems cheaper to implements the quantum arithmetical gates implementing $|x\rangle_n |0...0\rangle_m \to |x\rangle_n|f(x)\rangle_m$ although it requires much more work.