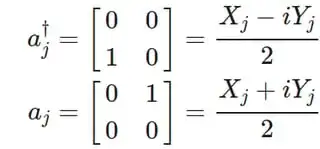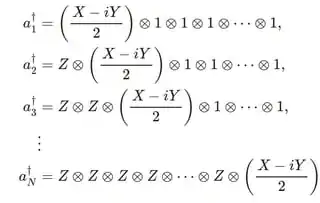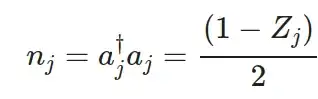Fermionic occupation operator and nearest neighbor Fermionic hopping interaction as a qubit operator

Question

How to express Fermionic occupation operator $(\hat{a}_j^\dagger\hat{a}_j)$ and nearest neighbor Fermionic hopping interaction ($H_h= J\sum_{i=1}\hat{a}_i^\dagger \hat{a}_{i+1}+\hat{a}_{i+1}^\dagger \hat{a}_{i})$ as a qubit operators.

Answer 1

• The oldest and most commonly known way is the Jordan-Wigner transformation. The qubit operators will be $\mathcal{O}(N)$-local for $N$ occupiable orbitals.
• A significantly more complicated way is the Bravyi-Kitaev transformation for which the qubit operators will be $\mathcal{O}(\log N)$-local.
• There's many other ways, but the above two are by far the most important to know in the early stages of your project.

You can simply transform creation and annihilation operators into "occupied" and "unoccupied" operators:

But you have to also make sure the wavefunction satisfies the anti-symmetric property for fermions, so you have to add strings of $Z$ operators to count the number -1's (this is the Jordan-Wigner transformation which is $n-local$):

The occupation operator in the first part of your question is simply:

To get the other operators in your question, you can just substitute the $a_j$ and $a^\dagger_j$ expression from above.

I used this source to get the equations.

Note that if your Hamiltonian has only nearest-neighbor couplings, then the issue of the JW transformation being $N$-local can be mitigated due to cancellation when multiplying (for example) $a_j$ with $a_{j+1}^\dagger$, as noted in Norbert Schuch's comment here.

Answer 2

Use the Jordan-Wigner transformation. For a 1D chain with NN interaction it will yield a spin Hamiltonian with NN interaction (specifically, the hopping will map to a XX term and the on-site term to a Z term). (In fact, part of this mapping is even given on the German Wikipedia site on the topic.)

On the other hand, if you don't want to put this on a quantum computer but solve it, you should stay in the fermionic picture (or map the spin problem to a fermionic one). This is how one solves e.g. the 1D quantum transverse field Ising model.

Finally, if you don't have 1D local Hamiltonians, considering other transformation which keep locality (or few-bodiness of the terms), such as the one mentioned in the other answer, can make sense (in particular since local spin models are easier to simulate than those with non-local and in particular many-body interaction).