Quantum implementation of arcsin

Question

I am looking to implement a quantum version of the arcsinus function. Such a problem is motivated by the HHL algorithm where $x\mapsto 1/x$ and $\arcsin$ can be used to get $1/x$ from the computational basis state into the amplitude.

My questions are based on the paper Optimizing Quantum Circuits for Arithmetic (arxiv link :https://arxiv.org/abs/1805.12445). Their idea is to use a polynomial approximation of the function $f$ and to partition the domain $\Omega$ of study of $f$ : $$ \Omega = \bigcup_{i=1}^M \Omega_i \quad \Omega_i\cap \Omega_j = \emptyset \, \forall i \neq j $$ and then perform a case distinction for each input, evaluating a different polynomial for $x\in \Omega_i$ and $y\in \Omega_j$, $i\neq j$. $M$ is chosen in order to achieve a certain precision and the degree of the polynomials are all bounded by a constant $d$.

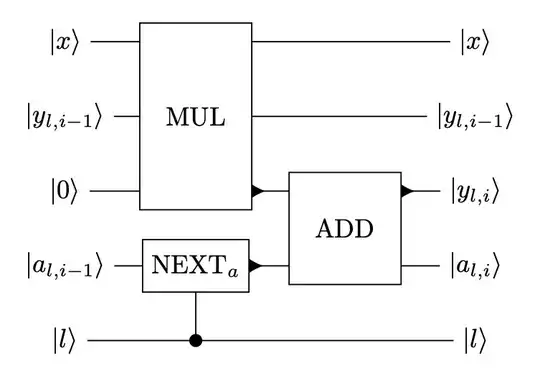
Evaluating a single polynomial $P(x) = \sum_{i=0}^d a_ix^i$ can be done using the Horner scheme, where one iteratively performs a multiplication by $x$ and an addition by $a_i$ for $i\in \{d, d-1, \cdots 0\}$ :

$$ a_d \mapsto a_dx+a_{d-1} \mapsto a_dx^2+a_{d-1}x + a_{d-2} \mapsto \cdots \mapsto P(x)$$

At iteration $i$, the last iterate is added by ${a_i}$, while this does not represent any difficulty in classical computing, a register has to hold the set of coefficients ${a_i}$, and has to be changed at each iteration. In their paper, the authors assume that $\mathrm{NEXT}_a$ implements such an operation.

My question : How can one implement efficiently the function $\mathrm{NEXT}_a$ ?

score 3 · Answer 1 · answered Jul 01 '21 at 09:37

Qiskit contains a method to approximate $\arcsin$ and other smooth functions using the techniques described in the mentioned paper (arXiv:1805.12445) in PiecewiseChebyshev class. A key component in the implementation is the PiecewisePolynomialPauliRotations class.

To use Qiskit's implementation:

import numpy as np
from qiskit import *
from qiskit.circuit.library.arithmetic.piecewise_chebyshev import PiecewiseChebyshev
number of state qubits:
N = 2
The function to be implemented:
func = lambda x: np.arcsin(1 / x)
degree = 2
breakpoints = [2, 4]
pw_approx = PiecewiseChebyshev(func, degree, breakpoints, N)
pw_approx._build()
num_ancilla_qubits = pw_approx.num_ancillas
qc = QuantumCircuit(pw_approx.num_qubits)
qc.h(list(range(N)))
qc.append(pw_approx.to_instruction(), qc.qubits)

If you want to go through the implementation details, you can access the source code from here: 1 & 2.

score 3 · Accepted Answer · answered Jul 01 '21 at 09:39

How can one implement efficiently the function $\text{NEXT}_a$?

According to the paper, $\text{NEXT}_a$ is just switching between loaded data that is indexed by the $\ell$ register:

$\text{NEXT}_a$ changes the register to hold the next set of coefficients $\sum \ell |\ell \rangle |a_\ell,i−1\rangle → \sum \ell |\ell \rangle |a_\ell,i−1\rangle$

In other words, there is some classical data that is indexed by a quantum register $\ell$ and a classical index $i$. We're unloading the data for index $i-1$ and loading the data for index $i$. (Alternatively, the difference between them is being xored into register.) Loading/unloading/xoring classical data indexed by a quantum register is done using what are called "QROM circuits".

There's a simple space efficient QROM defined in "Encoding Electronic Spectra in Quantum Circuits with Linear T Complexity"

I have a tested implementation of this QROM in Q-sharp on github.

If you have additional space available (including borrowed dirty qubits) you can use techniques from "Trading T-gates for dirty qubits in state preparation and unitary synthesis" to get the T count down from O(num_addresses) to O(sqrt(num_addresses * output_size)), assuming that's smaller.

It looks like there's also qsharp code for this one on github.

Quantum implementation of arcsin

2 Answers2

number of state qubits:

The function to be implemented: