How can I verify that the Pauli group is a group? And is it abelian?

Question

So how can I verify that the Pauli group is a group? Furthermore, is it Abelian? And then to sum it up, what is the order of the group? Trying to do some research into the Pauli group but I can't find much about it.

Answer 1

For the three Pauli matrices, {${\sigma_1,\sigma_2}=0$}, so certainly this can not form an abelian group. The Pauli group is an isomorphism with $D_4$.

The elements of the Pauli group are {${I, \sigma_x, \sigma_y, i\sigma_z, -I, -\sigma_x, -\sigma_y, -i\sigma_z}$}, so the order of this group is 8. In variant subgroups are {${I, -I}$}, {${I, -I, \sigma_{x/y}, -\sigma_{x/y}}$} and {${I, -I, i\sigma_z, -i\sigma_z}$}. $I$ and $-I$ is the only emelemt in its class. {$\pm\sigma_{x/y}$} and {$\pm i\sigma_z$} forms a class( totally 5 classes). Order 1 element: $I$. Order 2 elements: $\sigma_x, \sigma_2, -I, -\sigma_x, -\sigma_y$. And Order 3 elements: $\pm i\sigma_z$.

To check that the upper set actually forms a group, you need to prove that the set satisfies the four properties of a group: closure, associativity, identity element, inverse element, see Wikipedia for more detail.

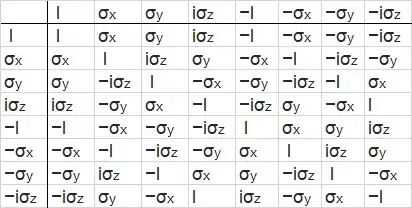
Here comes the group table of the Pauli group.

You can also see Wikipedia and check it is identical to the group table of $D_4$(in fact the tables are different because the ordering of elements is different).