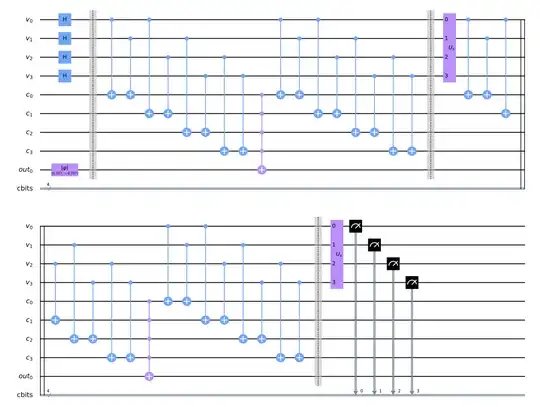
In this example implementation of Grovers Algorithm from the Qiskit Textbook which solves a $2\times 2$ sudoku puzzle:
https://qiskit.org/textbook/ch-algorithms/grover.html
The circuit iterates twice (see picture)
My question is:
How is the data in the $c_0 - c_3$ and out0 qubits utilised.
To me it looks like $c_0 - c_3$ and out are never fed back into the $v_0 - v_3$ qubits, and $v_0 - v_3$ are the only ones that are measured at the end.
I'm not sure if I've misinterpreted how entanglement works here, or how the CX gates work.