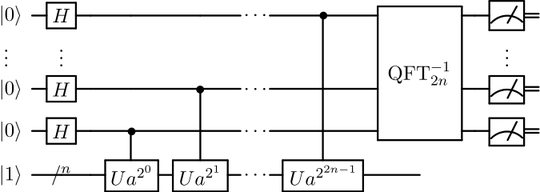
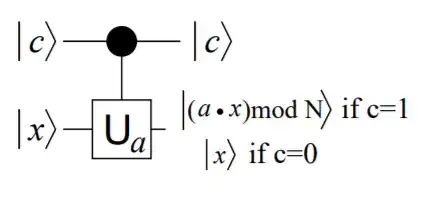I am trying to understand Shor's algorithm. I am not quite sure why the initialization, indicated as $|1\rangle$ in the below image at the bottom left is chosen as it is? I understand the modular exponentiation method in principle, but I am not sure which initialization should be chosen.
For preference, in a phase estimation algorithm, you would set the state of the second register equal to an eigenstate of the unitary operator $U$, the plan being to find its eigenvalue, which depends on the period $r$. In fact, any of the eigenvectors $|u_s\rangle$ would do for values $s=0,1,\ldots r-1$ as these have eigenvalues related to $s/r$.
However, the eigenstates themselves depend on $r$, so without knowing $r$, you cannot make the eigenstate, and so you cannot find $r$. That's a problem.
The way to circumvent the problem is that you can prepare the state $|1\rangle$, and it turns out that this state is an equal superposition of all the vectors $|u_s\rangle$. Using linearity, you now know the outcome - an equal superposition of the estimates of the different eigenvalues (entangled with the second register). Thus, in effect, what the phase estimation does is it measures one of the $s/r$ eigenvalues at random (with equal probability). (You then use the continued fractions algorithm to figure out which $s$ it was.)
The initial state of Shor's algorithm is $\frac{1}{\sqrt N}\displaystyle\sum_{a=0}^{N-1}|a\rangle$, and it is OK to move this state to $\frac{1}{\sqrt N}\displaystyle\sum_{a=0}^{N-1}|a,x\rangle$ as our initial state since the modular exponentiation takes $x$ as one of its input.
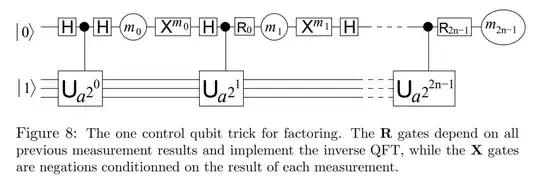
Here shows the model of a $\text{controlled}-U$ gate, and a circuit for factoring (figure comes from this paper).
So I think the $|x\rangle$ denoted here directs to $|x\rangle$, although I do not know why they are doing so.
