9

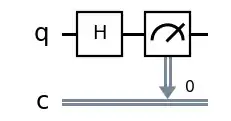
There are thousands of articles, books and web sites describing the Hadamard Gate from a theoretical point of view.

But I haven't been able to find any photo about any real implementeation of a Hadamard Gate on superconducting circuits nor any article describing how to make one.

Only some articles speaking about optical implementation of Hadamard gates. (An approach to realize a quantum Hadamard gate through optical implementation)

Maybe the following is the only one I've found with some information, though quite theoretical too (Realization of efficient quantum gates with a superconducting qubit-qutrit circuit)

How are the IBM and Google Hadamard gates fabricated (or created in the laboratory) and operated?

glS
  • 27,510
  • 7
  • 37
  • 125
skan
  • 193
  • 1
  • 5

3 Answers3

8

A Hadamard gate isn't usually a physical object that you pass qubits through. In the case of superconducting qubits, the Hadamard gate is performed by bouncing microwaves off of the qubits. It doesn't look like anything.

So you're not going to find a picture of a superconducting Hadamard gate on a chip. The closest thing to that would be one of the blips in this picture of the microwaves being sent down a line:

enter image description here

Craig Gidney
  • 44,299
  • 1
  • 41
  • 116
4

Fundamentally, a device such as an IBM quantum computer interacts according to a Hamiltonian, which might have some time-varying parameters. For example, for a single qubit, it might look like: $$ H=BZ+\Omega(t)X, $$ where $X$ and $Z$ are the standard Pauli matrices, and $B$ is a constant.

The goal is "simply" to specify the function $\Omega(t)$ to generate whatever unitary evolution you want according to the differential equation $$ i\frac{d|\psi\rangle}{dt}=H|\psi\rangle. $$

For the specific case of Hadamard, you can just set $\Omega(t)=B$ (assuming this is possible given the system constraints) for a fixed length of time $t_0$. Your evolution is then $$ U=e^{-iB(X+Z)t_0}=I\cos(B\sqrt{2}t_0)-i\sin(B\sqrt{2}t_0)\frac{X+Z}{\sqrt{2}} $$ So, if I pick $B\sqrt{2}t_0=\pi/2$, we get the evolution $$ U=-i\frac{X+Z}{\sqrt{2}}, $$ which is Hadamard up to an (irrelevant) global phase.

DaftWullie
  • 62,671
  • 4
  • 55
  • 140
2

If you wish to see how the microwave pulse in IBM's device, you can use their pulse schedule function to generate the pulse correspond to the circuit you are running. For example, if you run the circuitz;

enter image description here

then on the device, the qubit is being act on by the following microwave pulse:

enter image description here

More details can be found here on the qiskit documentation page

KAJ226
  • 14,182
  • 2
  • 12
  • 34