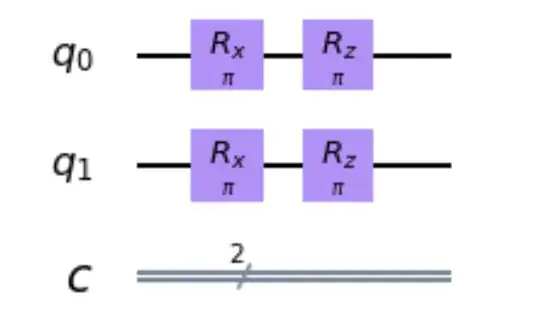
The circuit to simulate the term $e^{i Z \otimes Z t}$ can be construct as
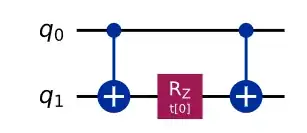
and the circuit to simulate the term $e^{i X \otimes Y t}$ can be construct as
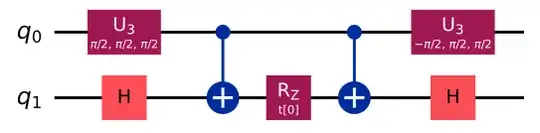
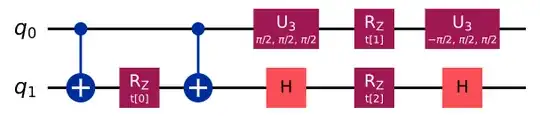
Now to simulate $H = X \otimes Y + Z \otimes Z$, we can use Trotter approx with one time slice to get the following circuit to approximate $e^{i (X \otimes Y + Z \otimes Z) t}$ :

Now as commented by @tsgeorgios, in fact, $X \otimes Y$ and $Z \otimes Z$ are commute. That is,
$$ [X\otimes Y, Z \otimes Z] = X\otimes Y \cdot Z \otimes Z - Z \otimes Z \cdot X\otimes Y = \boldsymbol{0}$$
you can see this explicitly as follows:
$$ X \otimes Y =
\begin{pmatrix}
0 & 0 & 0 & -i\\
0 & 0 & i & 0\\
0 & -i & 0 & 0\\
i & 0 & 0 & 0\\
\end{pmatrix} \ \ \ \ \ \ \textrm{and} \ \ \ \
Z \otimes Z =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & -1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 1\\
\end{pmatrix}
$$
hence you can see that $$ X \otimes Y \cdot Z \otimes Z - Z \otimes Z \cdot X \otimes Y = \begin{pmatrix}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
\end{pmatrix} $$
that is they are commute with one another. This is important because if two matrix $A$ and $B$ are commute then we have that (See here. )
$$e^{A + B} = e^{A}e^{B}$$
What this tells us is that the above circuit is the exact representation of the term $e^{i (X \otimes Y + Z \otimes Z) t}$ and not just an approximation!
Now, the circuit to simulate $e^{i X \otimes I t}$ is:
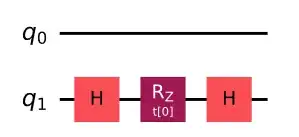
and the circuit to simulate $e^{i I \otimes Y t}$ is:
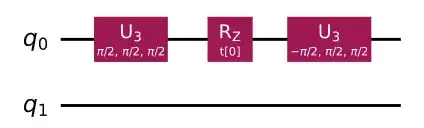
As you can see, the Identity operator doesn't do anything! so you can ignore them out of the circuit.
Thus, the trotter approx circuit for $e^{i (X \otimes I + I \otimes Y + Z \otimes Z) t}$ is:
I would like to linked a very good and detail answer by @Davit Khachatryan to a similar question here.