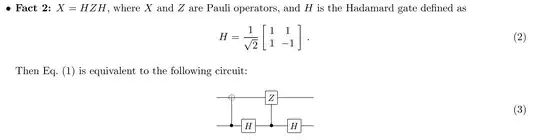
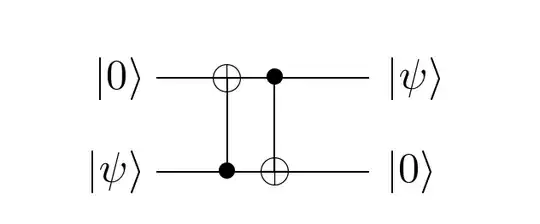
Here are three equivalent circuits:
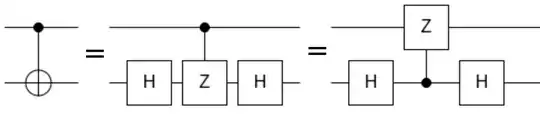
The second equation can be understood from this related answer about the fact that $CZ_{1 \rightarrow 2} = CZ_{2 \rightarrow 1}$, where first index is the control qubit and the second index is the target qubit. The first equation is similar to this related answer, but let's prove it explicitly where we will use $HZH = X$:
\begin{equation*}
I \otimes H \; (CZ_{1 \rightarrow 2}) \; I \otimes H=
\\ = I \otimes H \; (|0\rangle \langle 0 | \otimes I + |1\rangle \langle 1 | \otimes Z) \; I \otimes H =\\
= |0\rangle \langle 0 | \otimes H H + |1\rangle \langle 1 | \otimes HZH =
\\ = |0\rangle \langle 0 | \otimes I + |1\rangle \langle 1 | \otimes X = CNOT_{1 \rightarrow 2}
\end{equation*}
because $HH = I$ and $HZH = X$.