How to measure in another basis

Question

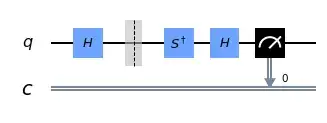
I am new to qiskit and I have to simulate a quantum circuit. I read this documentation https://qiskit.org/textbook/ch-states/single-qubit-gates.html where it is left as an exercise to the reader to write a function to measure in the $|+i\rangle$ and $|-i\rangle$ or the y-basis. I want to know if I've done it correctly or not.

I need to measure a state in the y-basis after preparing it in an equal superposition the $|0\rangle$ and $|1\rangle$ states. To do this, I first applied the Hadamard gate which does the first part and takes the $|0\rangle$ state to the $|+\rangle$ state. Now comes the measurement part. To do this I applied an $S^\dagger$ and then the $H$ gate again.

Now I simply measure the state

def Y_measurement(qc,qubit,cbit):
    qc.sdg(qubit)
    qc.h(qubit)
    qc.measure(qubit,cbit)
    return qc
circuit = QuantumCircuit(1,1)
circuit.h(0)
circuit.barrier()
Y_measurement(circuit, 0, 0)
circuit.draw(output='mpl') 

Is this correct?

Answer 1

Yes, your solution is correct.

Please find here circuits for measurement in z (computational), y (circular) and x (Hadamard) bases:

Source: Quantum Algorithm Implementations for Beginners, pg. 68.

Note that the blue Hadamard gate is used for preparing state $|+\rangle$ which is then measured. Pink gates are those needed for measuring in different basis. So, measurement in z basis needs no additional gate (left circuit), measuring in y basis needs $S^\dagger$ and $H$ additional gates (middle circuit) and measuring in x basis needs additional $H$ gate (right circuit).