Alternative derivation of $P(\text{First qubit}=0)$ for the swap test

Question

I'm trying to derive $P(\text{First qubit}=0) = \frac{1}{2} + \frac{1}{2}|⟨a|b⟩|^2$ for the swap test.

The wiki page shows one way, but the result should also be obtainable via direct expansion of the tensor products, as attempted here. Present question is about bringing this process to completion as I — rather disappointingly — wasn't able to finish the proof myself.

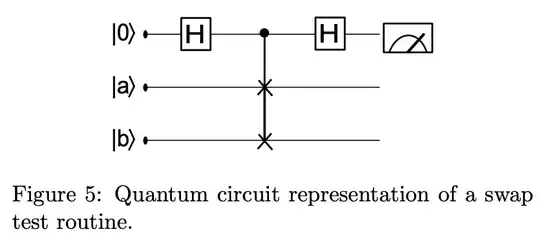
To summarize the thought process (adapted from here), let's assume we start out with:

$$ |a \rangle = a_0 |0\rangle + a_1 |1\rangle \\ |b \rangle = b_0 |0\rangle + b_1 |1\rangle \\ |\phi_0 \rangle = |0 \rangle |a \rangle |b \rangle $$

Applying $H$ to $|\phi_0\rangle$, we get:

$$ |\phi_1 \rangle = H|0\rangle|a\rangle|b\rangle = \frac{1}{\sqrt{2}}|0\rangle|a\rangle|b\rangle + \frac{1}{\sqrt{2}}|1\rangle|a\rangle|b\rangle $$

Applying the swap, we get:

$$ |\phi_2 \rangle = \frac{1}{\sqrt{2}}|0\rangle|a\rangle|b\rangle + \frac{1}{\sqrt{2}}|1\rangle|b\rangle|a\rangle $$

Applying the second H, we get:

$$ |\phi_3 \rangle = H|\phi_2\rangle = \\ \frac{1}{2}|0\rangle|a\rangle|b\rangle + \frac{1}{2}|1\rangle|a\rangle|b\rangle + \frac{1}{2}|0\rangle|b\rangle|a\rangle - \frac{1}{2}|1\rangle|b\rangle|a\rangle = $$ $$ \frac{1}{2}|0\rangle \left[|a\rangle|b\rangle + |b\rangle|a\rangle\right] + \frac{1}{2}|1\rangle \left[|a\rangle|b\rangle - |b\rangle|a\rangle \right] \tag{1}\label{1} $$

If we want to calculate $P(\text{First qubit}=0)$, then the interesting quantity from $|\phi_3\rangle$ is the first term of \eqref{1}:

$$ \frac{1}{2}|0\rangle \left[|a\rangle|b\rangle + |b\rangle|a\rangle\right] = \\ \frac{1}{2} \left[ 2 a_0 b_0 |0,0\rangle + \left( a_0 b_1 + a_1 b_0 \right) |0,1\rangle + \left( a_0 b_1 + a_1 b_0 \right) |1,0\rangle + 2 a_1 b_1 |1,1\rangle \right] = $$ $$ a_0 b_0 |0,0\rangle + \frac{1}{2} \left( a_0 b_1 + a_1 b_0 \right) |0,1\rangle + \frac{1}{2} \left( a_0 b_1 + a_1 b_0 \right) |1,0\rangle + a_1 b_1 |1,1\rangle \tag{2}\label{2} $$

Where I used: $$ |a \rangle |b \rangle = a_0 b_0 |0,0\rangle + a_0 b_1 |0,1\rangle + a_1 b_0 |1,0\rangle + a_1 b_1 |1,1\rangle \\ |b \rangle |a \rangle = a_0 b_0 |0,0\rangle + a_1 b_0 |0,1\rangle + a_0 b_1 |1,0\rangle + a_1 b_1 |1,1\rangle $$

Squaring the amplitudes from \eqref{2}, we get:

$$ |a_0 b_0|^2 + \frac{1}{4} | a_0 b_1 + a_1 b_0 |^2 + \frac{1}{4} | a_0 b_1 + a_1 b_0 |^2 + |a_1 b_1|^2 = $$ $$ |a_0 b_0|^2 + \frac{1}{2} | a_0 b_1 + a_1 b_0 |^2 + |a_1 b_1|^2 \tag{3}\label{3} $$

I'm trying to prove that \eqref{3} equals $\frac{1}{2} + \frac{1}{2}|⟨a|b⟩|^2$ but I could not. I tried using:

EDIT: The following equations do not hold, as explained by C. Kang in the answers.

$$ |\langle a| b \rangle|^2 = \langle a| b \rangle\langle a| b \rangle^\dagger = \langle a| b \rangle\langle b| a \rangle = \langle b| \langle a| b \rangle |a\rangle = |a_0 b_0|^2 + |a_1 b_0|^2 + |a_0 b_1|^2 + |a_1 b_1|^2 $$ $$ |a_0 b_0|^2 + |a_1 b_1|^2 = |\langle a| b \rangle|^2 - |a_1 b_0|^2 - |a_0 b_1|^2 \tag{4}\label{4} $$

Substituting \eqref{4} into \eqref{3}, I got:

$$ |\langle a| b \rangle|^2 - |a_1 b_0|^2 - |a_0 b_1|^2 + \frac{1}{2} | a_0 b_1 + a_1 b_0 |^2 $$

But I'm not sure how to turn this into $\frac{1}{2} + \frac{1}{2}|⟨a|b⟩|^2$. Any thoughts?

Answer 1

Welcome to the community Attila! I do not believe your equation 4 holds; consider the orthogonal vectors $ [\frac{i}{\sqrt{2}}, \frac{-i}{\sqrt{2}}]^T, [\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}]^T$ - their inner product should be 0 by orthogonality, but it can been seen that each of the terms you have would be nonzero, so their sum must be nonzero.

The correct expansion for (4) would be: $$ | \langle a | b \rangle |^2 = | \overline{a_0}b_0 + \overline{a_1}b_1 |^2 = (\overline{a_0} b_0 + \overline{a_1} b_1) \overline{(\overline{a_0}b_0 + \overline{a_1}b_1)} $$

Which, by distributivity of complex conjugation simplifies to:

$$ (\overline{a_0}b_0 + \overline{a_1}b_1)(a_0\overline{b_0} + a_1\overline{b_1}) = |a_0b_0|^2 + |a_1b_1|^2 + \overline{a_1 b_0} a_0 b_1 + \overline{a_0 b_1}a_1 b_0 $$

Let's also rewrite (3). Again, we can use the trick for the norm squared:

$$ |a_0 b_1 + a_1 b_0 |^2 = (a_0 b_1 + a_1 b_0)(\overline{a_0 b_1} + \overline{a_1 b_0}) = |a_0 b_1|^2 + |a_1 b_0|^2 + a_0 b_1 \overline{a_1 b_0} + a_1 b_0 \overline{a_0 b_1}$$

So, the entire (3) is:

$$ \frac{1}{2} (2|a_0 b_0|^2 + 2 |a_1 b_1|^2 + |a_0 b_1|^2 + |a_1 b_0|^2 + a_0 b_1 \overline{a_1 b_0} + a_1 b_0 \overline{a_0 b_1}) = \frac{1}{2}( |a_0 b_0|^2 + |a_0 b_1|^2 + |a_1 b_0|^2 + |a_1 b_1|^2 + |\langle a | b \rangle |^2)$$

Finally, recognize that $ |a_0 b_0|^2 + |a_0 b_1|^2 + |a_1 b_0|^2 + |a_1 b_1|^2 $ is actually just 1! (As it's the amplitudes of $|a \rangle |b \rangle$). Thus, we yield:

$$ \frac{1}{2} (1 + | \langle a| b \rangle |^2 )$$

As desired!