I know that $QFT_n|0\rangle$ is equivalent to $H_n|0\rangle$ (mathematical proof).
And it is also easy to prove that $QFT_1$ is equivalent to $H_1$ (applied to one QuBit).
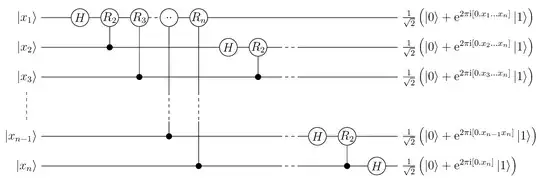
From looking at the circuit below it seems clear to me that the gates should also be equivalent if $|x_1\rangle$ is in any state and all other QuBits are $|0\rangle$. This should be true because none of the controlled $R$ gates are applied to $|x_1\rangle$.
I do not know how to prove this mathematically. Can anyone provide an elegant proof?