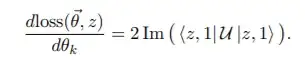We can use the SWAP test to determine the inner product of 2 states $|\phi\rangle$ and $|\psi\rangle$. The circuit is shown below 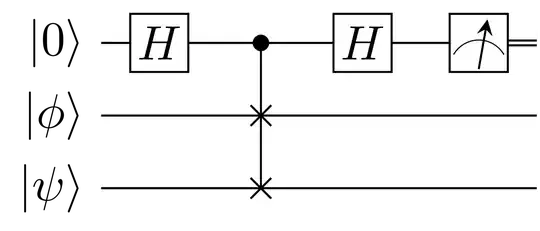
The state of the system at the beginning of the protocol is $|0\rangle \otimes |\phi \rangle \otimes |\psi \rangle$. After the Hadamard gate, the state of the system is $|+\rangle \otimes |\phi \rangle \otimes |\psi \rangle$.
The controlled SWAP gate transforms the state into $\frac{1}{\sqrt {2}}|0\rangle \otimes |\phi \rangle \otimes |\psi \rangle + |1\rangle \otimes |\psi \rangle \otimes |\phi \rangle$.
The second Hadamard gate results in
$$\frac {1}{2}(|0\rangle|\phi\rangle|\psi\rangle +|1\rangle|\phi\rangle|\psi\rangle +|0\rangle|\psi\rangle|\phi\rangle -|1\rangle|\psi\rangle|\phi\rangle ) \\
=\frac {1}{2}|0\rangle (|\phi\rangle|\psi\rangle +|\psi\rangle|\phi\rangle)+ \frac{1}{2}|1\rangle(|\phi\rangle|\psi\rangle -|\psi\rangle|\phi \rangle)$$
The Measurement gate on the first qubit ensures that it's 0 with a probability of
$P(\text{First qubit}=0)=\frac {1}{2}\Big(\langle\phi|\langle\psi| + \langle\psi|\langle\phi|\Big ) \frac {1}{2}\Big (|\phi\rangle|\psi\rangle + |\psi\rangle |\phi\rangle \Big )=\frac {1}{2}+\frac {1}{2}|\langle\psi|\phi\rangle|^{2}$ when measured.
The downside of this test is that the qubits cannot be recovered to the same state as before. Hence $|\psi\rangle,|\phi\rangle|$ must be prepared multiple times independently in order to get a good probability estimate and hence the value of inner product.