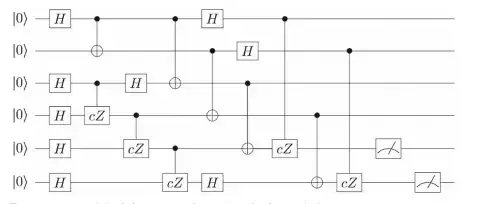
The calculation of the resulting state of the described circuit:
After applying the same circuit identities described in this answer (and here) to the connected question we will obtain a "simplified" circuit:
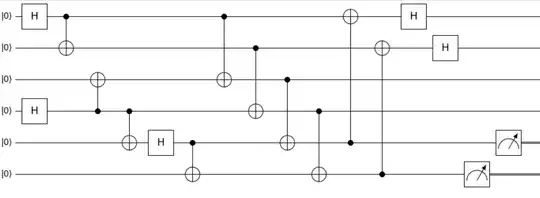
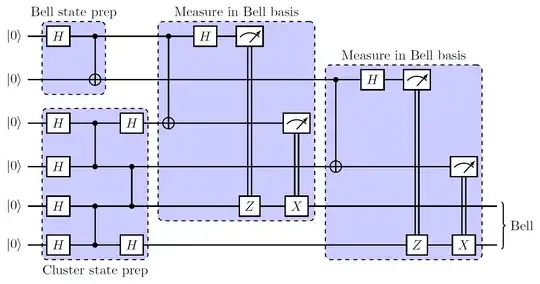
Here are the links to the initial, first intermediate, second intermediate and final circuits presented in the Quirk. Whenever it was possible (by commuting relations of the gates) and convenient the places of the gates were changed. For example adjacent CNOTs on different pairs of qubits can change their positions. In the first part discussed here combined with the Bell state we will have the following state:
$$| \psi_1 \rangle = \frac{1}{2\sqrt{2}} \big(|00\rangle + |11\rangle\big)\big(| 0000 \rangle + | 0011 \rangle + | 1100 \rangle - | 1111 \rangle \big)$$
After the following "cascade-like" sequence consisted of $4$ CNOTs:
$$| \psi_2 \rangle = \frac{1}{2\sqrt{2}} \Big(| 000000 \rangle + | 000011 \rangle + | 001111 \rangle - | 001100 \rangle +
\\ + | 111111 \rangle + | 111100 \rangle + | 110000 \rangle - | 110011 \rangle \Big)$$
After the final two CNOTs:
$$| \psi_3 \rangle = \frac{1}{2\sqrt{2}} \Big(| 000000 \rangle + | 110011 \rangle + | 111111 \rangle - | 001100 \rangle +
\\ + | 001111 \rangle + | 111100 \rangle + | 110000 \rangle - | 000011 \rangle \Big)$$
After the final two Hadamard gates:
$$| \psi_4 \rangle = \frac{1}{2\sqrt{2}} \Big(| ++0000 \rangle + | --0011 \rangle + | --1111 \rangle - | ++1100 \rangle +
\\ + | ++1111 \rangle + | --1100 \rangle + | --0000 \rangle - | ++0011 \rangle \Big)$$
We can simplify this state:
$$| \psi_4 \rangle = \frac{1}{2\sqrt{2}} \Big(| 000000 \rangle + | 110000 \rangle - | 010011 \rangle - | 100011 \rangle +
\\
+ | 001111 \rangle + | 111111 \rangle - | 011100 \rangle - | 101100 \rangle \Big)$$
Regrouping the terms:
$$| \psi_4 \rangle = \frac{1}{2\sqrt{2}} \Big(\big(| 0000 \rangle + | 1100 \rangle - | 0111 \rangle - | 1011 \rangle \big) |00\rangle +
\\
+ \big(| 0011 \rangle + | 1111 \rangle - | 0100 \rangle - | 1000\rangle \big) |11\rangle \Big)$$
This is the final state that should be measured (only the last two qubits). This final result can be checked from Quirk's output that can be found from the initial version of the circuit (the order of the qubits in the ket notation is reversed there).