In Nielsen and Chuang, it is stated that the effect of phase estimation circuit is mapping state $|j\rangle |u\rangle$ to $|j\rangle U^j |u\rangle$. 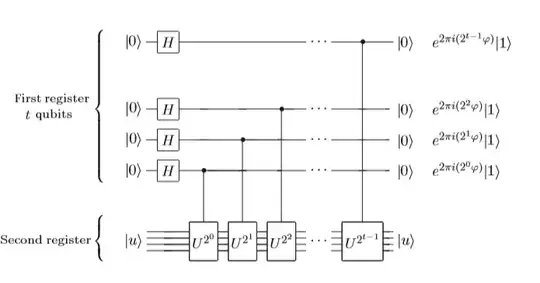
Here is my solution: Consider the first $CU^{2^0}$. Let $|j\rangle = |j_1j_2\dots j_t\rangle$. It maps the state $|j\rangle |u\rangle$ to state $|j\rangle U^{j_t2^0}|u\rangle$.If $j_t=0$, then nothing happens. Otherwise, $U^{2^0}$ is applied.
Continuing like this I get the following quantum state:
$|j\rangle U^{j_12^{t-1}} \cdots U^{j_t2^0}|u\rangle$
Then it should be true that $U^{j_12^{t-1}} \cdots U^{j_t2^0} = U^j$ but I cannot see how this follows. I am studying order finding algorithm and modular exponentiation part heavily depends on this observation. Can someone help?